
Из-за двух равных сторон, равнобедренный треугольник обладает рядом специфических свойств, за которые его очень любят составители задач. Рассмотрим, чем же выделяется высота равнобедренного треугольника и как ее лучше найти.
Определение
В общем случае, высота – это перпендикуляр, опущенный из вершины фигуры на противолежащую сторону. В равнобедренном треугольнике под высотой обычно подразумевают высоту, опущенную на основание.
Если по условию задачи нужно найти значение высоты равнобедренного треугольника без уточнений, какую именно требуется найти, то имеется в виду высота, опущенная на основание.
Необходимые теоремы
Для решения задач на определение высоты равнобедренного треугольника, нужно знать теорему Пифагора и свойство высоты равнобедренного треугольника.
Теорема Пифагора: в прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов.
Свойство: в равнобедренном треугольнике высота, проведенная к основанию, является медианой и биссектрисой.
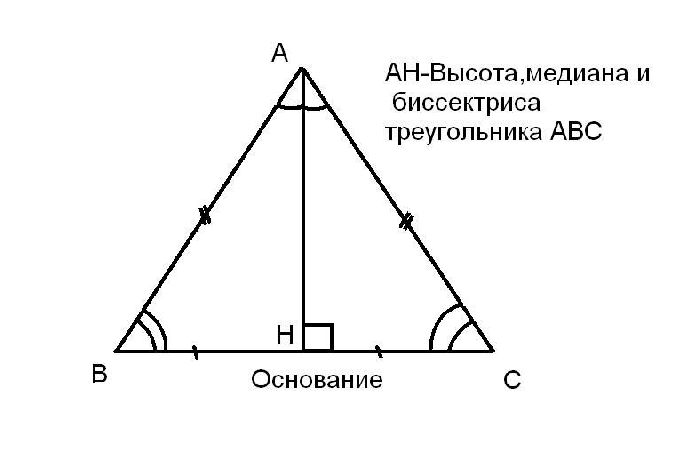
Из теоремы и свойства следует основная формула высоты равнобедренного треугольника. Рассмотрим равнобедренный треугольник АВС с высотой АН и основанием ВС. Тогда треугольник АВН является прямоугольным. Запишем значение высоты через теорему Пифагора, так как в треугольнике АВН высота АН является катетом.
$$АН=sqrt{АВ^2-BH^2}=sqrt{AB^2-({BC\over{2}})^2}$$
$$ВН={1\over2}*ВС$$, так как по свойству высоты равнобедренного треугольника АН является медианой. Это и есть формула высоты равнобедренного треугольника.
Задача
Решим задачу, где будет задействована не только высота, проведенная к основанию, но и другая высота. В равнобедренном треугольнике, как и в любом другом, их три. В задаче также будет применен способ нахождения высоты, который можно использовать для любого треугольника, а не только для равнобедренного.
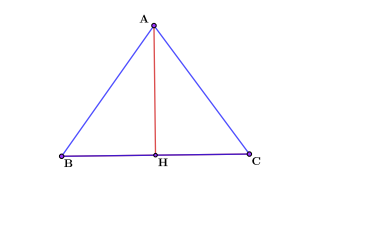
В Равнобедренном треугольнике АВС с основанием ВС проведены высоты АН и ВР. Синус угла АСВ равен 0,6, а боковая сторона 5. Найти высоту ВР.
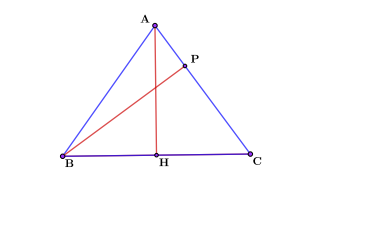
Для начала, необходимо найти значение высоты, проведенной к основанию и основание. Для этого обратим внимание на прямоугольный треугольник АСН. Воспользуемся определением синуса.
Синус угла это отношение противолежащего катета к гипотенузе. Нам известно значение синуса, значит:
$${АН\over{АС}}=0,6$$ – из этого отношения выразим значение АН.
$$АН=0,6 *АС=0,6*5=3$$
Через теорему Пифагора найдем значение НС:
$$НС=sqrt{АС^2-AH^2}=sqrt{25-9}=sqrt{16}=4$$
Тогда основание равно:
$$ВС=ВН+НС=2*НС=2*4=8$$
Теперь найдем площадь треугольника:
$$S={1\over2}*АН*ВС={1\over2}*3*8=12$$
С другой стороны площадь можно найти и через высоту ВР.
$$S={1\over2}*ВР*АС$$ – так как ВР это высота, проведенная к стороне АС.
Значит верно равенство:
$${1\over2} *АН*ВС={1\over2}*ВР*АС$$
$$АН*ВС=ВР*АС$$
$$ВР={{АН*ВС}\over{АС}}={{3*8}\over5}={24\over5}=4,8$$
Что мы узнали?
Мы вывели формулу высоты прямоугольного треугольника. Определили, что высота в прямоугольном треугольнике может находиться любым способом, связанным с произвольным треугольником и решили интересную задачу на нахождение высоты треугольника.








Комментирование закрыто