
Правильный треугольник обладает множеством специфических свойств, которые значительно упрощают решение задач. Поэтому имеет смысл поговорить о каждом из этих свойств, чтобы облегчить решение задач.
Определение
Правильный треугольник – это треугольник, у которого все стороны равны и каждый угол равен 60 градусам. Правильный треугольник еще называют равносторонним. О формулах правильного треугольника и о том, как производить с их помощью различные расчеты, мы поговорим ниже.
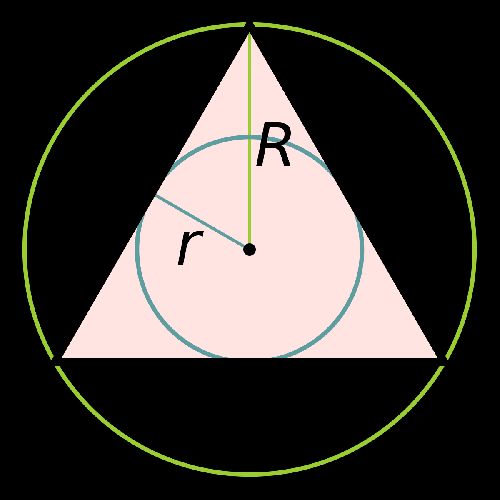
Формулы правильного треугольника
Почти все формулы следуют из утверждения, что правильный треугольник имеет 3 угла по 60 градусов и 3 равные стороны.
Площадь
Начнем с формулы площади.
Равносторонний треугольник любой высоты делится на два равных прямоугольных треугольника. Теперь найдем значение высоты, заменим его классической формулой площади треугольника и получим формулу нахождения площади правильного треугольника.
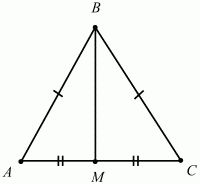
В прямоугольном АВМ катет ВМ можно выразить через синус угла БАМ. Этот угол известен и равен 60 градусам, а значит, известны и значения синуса и косинуса этого угла. Так как ВМ противоположна, а это значит, что для ее нахождения нужно воспользоваться формулой синуса.
$$Sin(ВAM)={ВM\над AB}$
С другой стороны, синус 60 градусов известен заранее и равен $\sqrt{3} \over 2$ . Таким образом, мы можем выразить значение AM:
$$ВМ=АВ*sin(ВAM)=AB* {\sqrt{3}\over 2}$
Все стороны треугольника равны между собой, поэтому для простоты обозначим их буквой а.
AB=AC=BC=а
Тогда формула будет выглядеть так:
$$VM=a*{\sqrt{3}\over2}$
Теперь вспомним классическую формулу площади треугольника:
$S= {1\over2}h*a$, где a — основание треугольника, h — высота, проведенная к этому основанию. В данном треугольнике это будет выглядеть так:
$$S={1\over2}*AC*BM={1\over2}*a*a*{\sqrt{3}\over2}=a^2*{\sqrt{3}\over4}$
Полученная формула значительно проще классических по количеству требуемых параметров. Чтобы найти площадь правильного треугольника, достаточно знать значение одной из сторон. Это возможно из-за подобия углов такого треугольника.
Только в правильном треугольнике возможно нахождение площади через значение одной стороны.
Периметр
Периметр найти еще проще, так как он представляет собой сумму всех сторон треугольника, и все они равны между собой, тогда:
Р=3а
Подобный подход, при котором стороны выравниваются или используются свойства медиан и биссектрис равностороннего треугольника, часто применяется при решении подобных задач. Правильный треугольник не имеет и не может иметь объема, поскольку является плоской фигурой. Ему присущи два характерных понятия: площадь и периметр.
В равностороннем треугольнике каждая биссектриса совпадает с медианой и высотой. Также совпадают и точки пересечения этих отрезков. Получившаяся точка зовется центром фигуры.
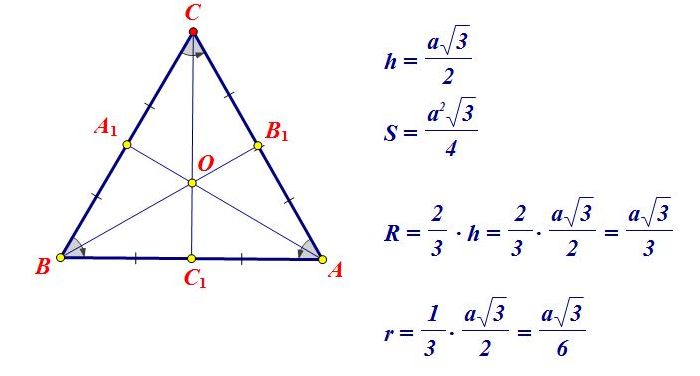
Что мы узнали?
Из статьи мы узнали, что у правильного треугольника все стороны и углы равны между собой. Мы узнали о свойствах биссектрисы, медианы и высоты – в правильном треугольнике это будут одни и те же линии. Его можно выполнить из любой вершины.








Комментирование закрыто