
Средняя линия прямоугольного треугольника — прекрасная возможность для авторов проблем. Большинство учащихся знают, что такое центральная линия, и умело используют ее свойства при решении. Но как только на рисунке прямоугольного треугольника появляется этот отрезок, они тут же впадают в ступор из-за чего-то необычного в рисунке, поэтому давайте рассмотрим тему подробнее.
Что такое прямоугольный треугольник?
В общем, треугольник – это фигура, состоящая из трёх сторон и трёх углов. В зависимости от величины углов, входящих в треугольник, различают:
- Остроугольные треугольники, все углы которых меньше 90 градусов.
- Тупоугольные треугольники, у которых один из углов больше 90 градусов.
- Прямоугольные треугольники, один угол которых равен 90 градусам.
Прямоугольные треугольники интересны своими особыми формулами, которые значительно упрощают решение. Но средняя линия прямоугольного треугольника ничем не отличается от средней линии любого треугольника. Почему проблемы с этим сегментом сложны? Только из-за необычного дизайна
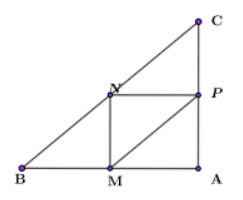
Средняя линия
Что такое средняя линия? Это один из характеризующих сегментов любого треугольника. Центральная линия соединяет середины соседних сторон многоугольника.
Средняя линия есть не только у треугольника. Она существует у каждой выпуклой фигуры. При этом свойства средних линий треугольников не всегда совпадают с свойствами средних линий трапеций. Поэтому будьте аккуратны, у каждой фигуры есть свои свойства и признаки.
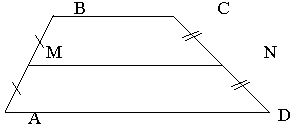
Свойства средней линии
У средней линии не так много особенностей, но все они более чем интересны.
- Центральная линия всегда параллельна стороне, через которую она не проходит. В противном случае говорят, что средняя линия параллельна основанию. Это облегчает запоминание этого свойства, но немного страдает формулировка. Дело в том, что в любом треугольнике можно провести 3 центральные линии, но это только основа, поэтому будьте осторожны с формулировкой.
- Центральная линия равна половине основания. Вернее, не основания, а стороны, которые не пересекает центральная линия. Это формула средней линии любого треугольника, включая прямоугольный.
- Средняя линия пересекает треугольник, подобный оригиналу с коэффициентом подобия 1:2
Если формулировка «Средняя линия параллельна основанию» не совсем правильная, то почему же ее применяют в учебнике? Дело в том, что любое свойство должно быть коротким и ясным для простоты запоминания. Поэтому и сокращают некоторые высказывания. А основанием произвольного треугольника можно считать любую сторону, а значит неправильной формулировку назвать нельзя.
Задача
В прямоугольном треугольнике ABC три средние линии: MN; НП; М.П. В получившемся прямоугольнике МНПА известно, что синус угла между диагоналями равен 0,5. А средние линии MN и NP равны соответственно 3 и 4. Найдите площадь большого прямоугольного треугольника.
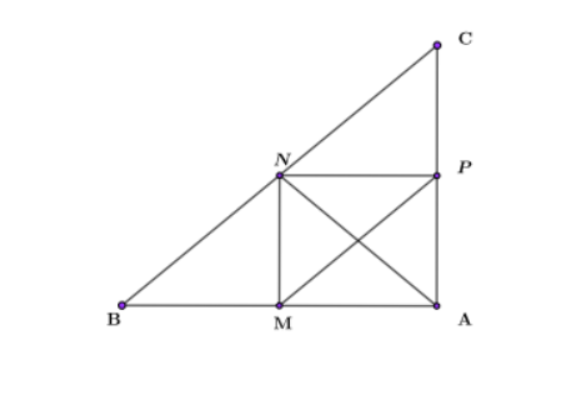
В прямоугольнике две диагонали равны друг другу. Одна из диагоналей MP является гипотенузой прямоугольного треугольника MNP. Катеты треугольника известны, а значит, гипотенузу можно найти по теореме Пифагора.
$$MP=\sqrt{MN^2+NP^2}=\sqrt{9+16}=\sqrt{25}=5$
Найдём площадь прямоугольника как произведение диагоналей на синус угла между ними.
$$S=5*5*0,5=12,5$
В большом треугольнике 4 маленьких треугольника, в прямоугольнике 2 маленьких треугольника. Все маленькие треугольники подобны, а это значит, что чтобы найти площадь прямоугольного треугольника, необходимо площадь прямоугольника умножить на 2.
$S=12.5*2=25$ — ответ получен.
Что мы узнали?
Мы узнали, что такое средняя линия прямоугольного треугольника. Мы рассказали о свойствах центральной линии и решили небольшую задачу по закреплению материала.








Комментирование закрыто