
Стороны равнобедренного треугольника найти довольно легко – нужно лишь выработать навык и научиться пользоваться теоремами об этой фигуре, которых не так много. Поговорим о каждой из сторон треугольника и о том, как ее определить отдельно.
Равнобедренный треугольник
Равнобедренный треугольник – это треугольник, у которого две стороны равны, а третья – основание.
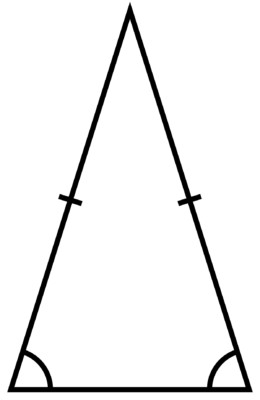
Только в равнобедренном треугольнике основание имеет реальное практическое применение. Для лучшего визуального восприятия фигуры стоит располагать чертеж так, чтобы основание располагалось внизу. Это не принципиальный вопрос и иногда решение вынуждает нас располагать фигуру иначе, но если есть возможность, то стоит поместить основание внизу фигуры.
Свойства равнобедренного треугольника
Свойства равнобедренного треугольника не так уж и велики. Для решения школьных задач даже в старших классах используются всего 3 свойства:
- Стороны треугольника равны.
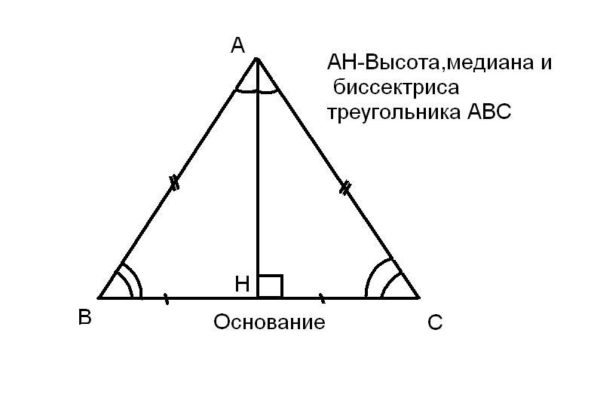
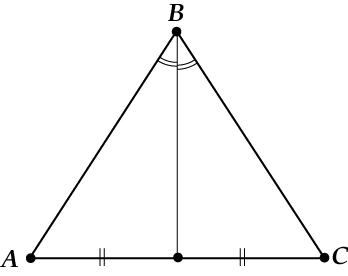
- Биссектриса треугольника совпадает с медианой и высотой.
- Углы при основании равнобедренного треугольника равны.
Этих свойств вполне достаточно, чтобы использовать стиль решения, неприменимый ни к одному другому треугольнику.
Стороны равнобедренного треугольника
Равнобедренный треугольник отличается от других фигур тем, что для решения всего треугольника достаточно двух показателей, из которых хотя бы один должен быть стороной.
Например, если известны сторона и угол при основании, можно провести медиану; она будет совпадать с биссектрисой и высотой, разделяя треугольник на два небольших равных прямоугольных треугольника.
В этих треугольниках известна гипотенуза, которая является одновременно стороной равнобедренного треугольника и прилежащим к ней углом. Это значит, что через тригонометрическую функцию известного угла, т е через синус или косинус, можно найти каждый из катетов.
Одна из катетов — биссектриса, высота и медиана. Другой — половина базы. Почему половина? Потому что часть сегмента, то есть ножка, отрезана от основания сегмента, которое можно считать медианой. А медиана — это отрезок, соединяющий вершину с центром противоположной стороны.
Тригонометрическую функцию известного угла можно определить по таблицам Брадиса. В этих таблицах рассчитаны значения для всех существующих целых и промежуточных углов.
Как найти оставшийся третий угол? Использует те же тригонометрические функции. В маленьком прямоугольном треугольнике известен один угол — угол при основании равнобедренного треугольника. В прямоугольном треугольнике сумма острых углов равна 90 градусов, то есть из 90 вычитаем известную величину и получим половину угла, противоположного основанию.
Почему половина? Потому что высота, образующая два равносторонних треугольника, тоже является биссектрисой. Поэтому полученное значение необходимо умножить на два и получить результат.
Равнобедренный треугольник не может быть решен, если:
- Известны только 2 стороны.
- Известны только углы.
- Известен только фундамент.
- Известно лишь значение некоторых характеризующих отрезков: высоты, медианы, биссектрисы и т д.
Во всех остальных случаях треугольник разрешим. Зачем знать варианты, когда решение заведомо невозможно? Чтобы не попасть в ловушку неразрешимых проблем. Это редкость, но они случаются. Предлагая их к решению, составители проверяют уровень знаний учащихся о рисунке.
Что мы узнали?
Мы рассказали о том, что такое равнобедренный треугольник, выделили его основные свойства и поговорили о формулах сторон равнобедренного треугольника.








Комментирование закрыто