
Внешний угол треугольника – тема, помогающая комплексно воспринимать треугольник. Изучая внешние углы, ученик понимает, что для облегчения решения задачи можно использовать дополнительные конструкции.
Угол
Что такое угол? Угол – это два луча, исходящие из одной точки. Угол – это степень поворота одного луча относительно другого. Минимальный угол достигается при совпадении двух лучей. Этот угол считается нулевым. Углы полные, прямые, острые и тупые.
Смежные и вертикальные углы
Чтобы понять тему внешнего угла, вам необходимо обсудить понятия смежного и вертикального углов. Вертикальные углы – это углы, стороны которых являются продолжением друг друга. Такие углы всегда равны. При пересечении двух прямых образуются две пары вертикальных углов.
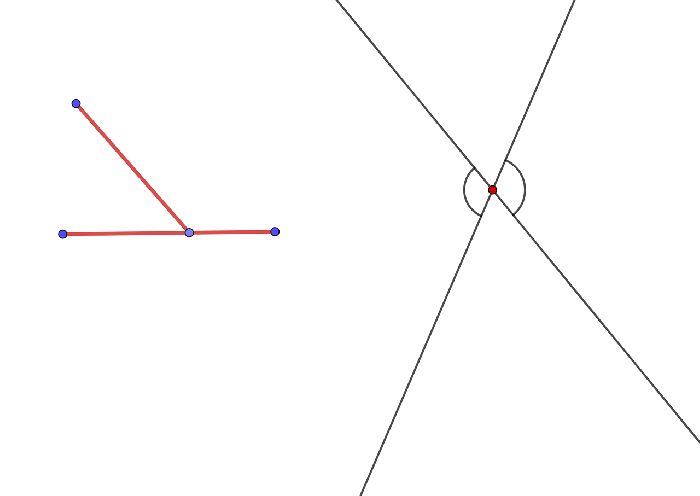
Смежные углы – это углы, у которых одна сторона является продолжением другой, а другая является общей. Два таких угла вместе образуют перевернутый угол 180 градусов. Это означает, что сумма смежных углов равна 180 градусов.
Вертикальные углы часто используются в доказательствах, а смежные можно применять при решении задач с дополнительным построением.
Внешний угол
Внешние углы существуют не только в треугольниках. Этот угол можно добавить к любой фигуре. Для этого необходимо одну из сторон фигуры продолжить, тогда другая сторона образует этим продолжением два смежных угла.
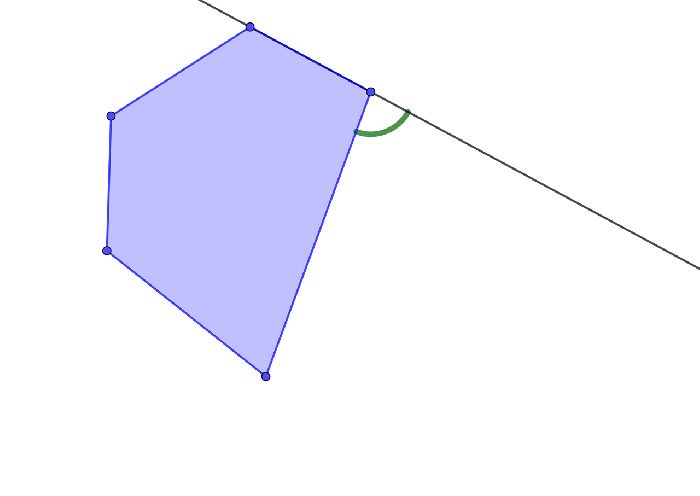
В любой вершине фигуры всегда пересекается 2 стороны. Значит, можно получить две прямые, которые являются продолжением этих сторон и внешних углов при каждой вершине может быть 2.
Внешний угол треугольника
Внешний угол треугольника — единственный из всех внешних углов, обладающий набором определенных свойств, которые могут помочь в решении задач.
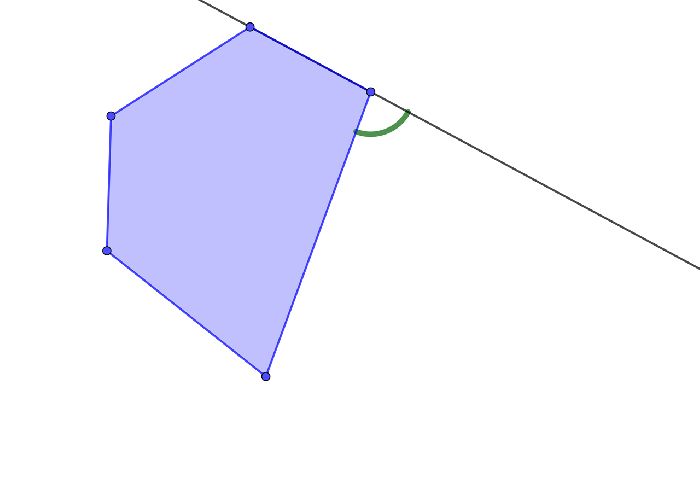
Но прежде всего стоит сказать, что редко в решении нужны два внешних угла с одной вершиной. Это особо сложные задачи, часто олимпиадного уровня. Поэтому в целом не стоит портить рисунок и строить две пары смежных углов.
Теперь покажем свойства внешних углов треугольника:
- Внешний угол треугольника равен сумме внутренних углов, не примыкающих к нему. Это свойство используется чаще других и поэтому считается основным свойством внешнего угла. Но есть и другие.
- Сумма трех внешних углов, по одному при каждой вершине треугольника, равна 360 градусам.
- Если построить два смежных угла при одной вершине, они будут вертикальными.
Что мы узнали?
Мы подробно исследовали тему внешнего угла треугольника. Мы разделили понятия смежных и вертикальных углов, указали, какой из углов внешнего угла будет смежным, а какой вертикальным. Мы поговорили об известных и неизвестных свойствах внешних углов и обсудили функции построения внешних углов в треугольнике.








Комментирование закрыто