
Среди всех фигур выделяется равносторонний треугольник: в нем легко найти значение всех сторон и углов, так как все углы известны заранее, и, найдя одну сторону, можно найти все три одновременно. Но именно из-за этих особенностей авторы задач любят писать сложные условия, которые не всегда можно понять с первого раза, например, не всегда можно понять, что такое медиана, потому что человеку легче воспринять понятие высота, чем медиана. Рассмотрим понятие медианы в равностороннем треугольнике подробно.
Определения
Равносторонний треугольник – это треугольник, у которого все стороны равны и углы 60 градусов.
Равносторонний треугольник это частный случай равнобедренного, но в равностороннем любую сторону можно считать основанием.
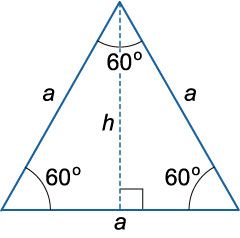
Отсюда следует, что каждая высота равностороннего треугольника является медианой и биссектрисой, поскольку каждая высота проведена к стороне, которую можно считать основанием.
Медиана – это отрезок, соединяющий вершину треугольника с серединой противоположной стороны. Медиана также обладает рядом свойств, которые можно использовать для решения задач.
Медианы треугольника пересекаются в одной точке и делят эту точку в соотношении 2:3, считая от вершины. В данном случае медианы делят треугольник на 6 треугольников разной величины. Если посмотреть на картинку, то можно увидеть, что в равностороннем треугольнике каждый из этих 6 треугольников будет прямоугольным.
Формула медианы равностороннего треугольника
Выведем формулу медианы равностороннего треугольника. В равностороннем треугольнике ABC проведем высоту AN. Это также будет медиана и высота. Медиана разделит треугольник на два прямоугольника: ANS и ANV. Рассмотрим треугольник ANS.
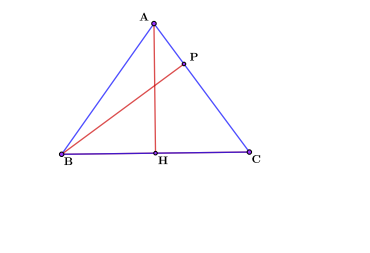
Здесь мы используем теорему Пифагора:
$$AC^2=AH^2+HC^2$
$$AH=\sqrt{AB^2-BH^2}$
Обозначим каждую сторону буквой А. Итак, AB=a; $$ВН={а\over2}$
$$AN=\sqrt{a^2-{a\over2}^2}=\sqrt{a^2-{a^2\over4}}$
Это формула медианы равностороннего треугольника. С другой стороны, вы можете использовать тригонометрические тождества и вывести другую формулу:
$$sin(ACH)={AH\over AC}$
В данном случае угол ACH составляет 60 градусов. Это значит, что мы можем определить синус угла: $$sin(ACH)={\sqrt{3}\over 2}$
Выразим значение медианы AN
$$AN=sin(ACH)*AC={\sqrt{3}\over2}*AC={\sqrt{3}\over2}*a$
Вот еще одна формула, типичная для равностороннего треугольника.
Задача
Чтобы закрепить тему, давайте решим простую задачу, связанную с обратной формулой медианы.
В равностороннем треугольнике медиана равна $$20\over{\sqrt{3}}$$. Найдите площадь треугольника.
Для нахождения площади воспользуемся классической формулой.
Классическую формулу можно использовать для нахождения площади любого треугольника.
Для этого нам нужны значения стороны и высоты. Высота равностороннего треугольника совпадает с медианой, поэтому нужно просто найти сторону. Выразим это через формулу медианы равностороннего треугольника.
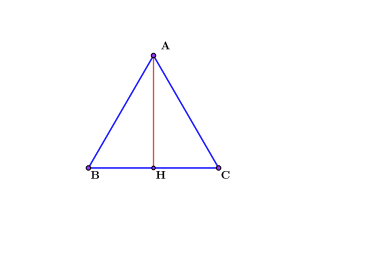
$$m={\sqrt{3}\over2}*a$
$$a={m\over{\sqrt{3}\over2}}=m*{2\over\sqrt{3}}$
Подставим медианное значение в формулу:
$$a={20\over\sqrt{3}}*{2\over\sqrt{3}}={40\over3}$
Давайте посчитаем площадь:
$$S={1\over2}*a*m={1\over2}*{40\over3}*{20 \over\sqrt{3}}={400\over{3\sqrt{3}}}$
Что мы узнали?
Мы вывели две формулы медианы равностороннего треугольника, дали определения, необходимые для решения задач, и решили небольшую задачку для закрепления знаний.








Комментирование закрыто