
Медиана – один из уникальных отрезков треугольника. Медиана обладает рядом свойств, полезных для решения задач, а пересечение медиан еще больше расширяет список этих свойств. О пересечении медиан и его свойствах пойдет речь сегодня.
Медиана
Медиана — это отрезок, соединяющий вершину треугольника с серединой отрезка на противоположной стороне. Три медианы треугольника пересекаются в одной точке, которая называется медианным пересечением.
Медианы, в отличие от высот, всегда лежат внутри треугольника. Это логично, ведь медианный отрезок соединяет вершину и центр страницы. А центральная точка страницы всегда находится внутри треугольника.
Если соединить два любых основания медиан отрезком, то получится средняя линия треугольника. Три средние линии треугольника образуют треугольник, подобный изначальному с коэффициентом подобия 1:2
Есть еще одно интересное свойство медиан, которое поможет вам избежать путаницы при построении золотого сечения треугольника. Медиана треугольника всегда расположена между высотой и биссектрисой (за исключением равнобедренных и равносторонних треугольников).
Вот формула для расчета длины медианы трех сторон. Эту формулу часто используют при решении задач, поэтому ее стоит запомнить.
$$m_c={{\sqrt{2a^2+2b^2-c^2}}\over{2}}$
Зачастую ученикам проще запомнить словесную формулировку, а не заучивать формулу. Чтобы найти медиану по трем сторонам, нужно взять корень из сумм удвоенных квадратов сторон минус квадрат стороны, к которой проведена медиана. Полученный корень нужно поделить пополам.
Точка пересечения медиан
Точка пересечения медиан является одной из трех примечательных точек треугольника, составляющих золотое сечение треугольника.
Пересечение медиан треугольника обладает рядом свойств, полезных для решения задач:
- Медиана разбивается на отрезки пересечения в соотношении 2:1, начиная с вершины.
- Три медианы, проведенные в треугольнике, делят его на 6 равных треугольников. Треугольники равной площади называются равновеликими. Сами эти цифры имеют мало общего, но их числовые характеристики площади совпадают.
- Точка пересечения медиан в треугольнике называется центроидом и является центром тяжести треугольника.
Пересечение медиан — единственное из золотого сечения треугольника, имеющее реальный физический смысл. Если вырезать из картона треугольник и провести в нем тонким карандашом медианы, то точка их пересечения будет центром тяжести плоской фигуры.
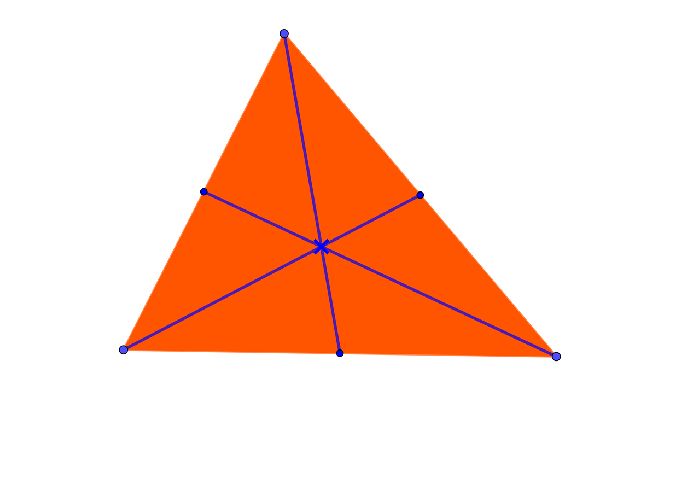
Это значит, что если в эту точку поместить булавку, фигурка останется на ней, не прокалываясь, просто за счет баланса.
Что мы узнали?
Мы дали формулу для расчета медианы трех сторон треугольника. Приведены некоторые свойства пересечения медиан в треугольнике. Мы говорили о реальном физическом смысле центроида треугольника.








Комментирование закрыто