
Сложение и вычитание векторов – одна из немногих операций на стыке математики и геометрии. Дело в том, что выражения из векторов можно складывать и вычитать арифметически, ориентируясь только на буквенные обозначения векторов, но для получения числового результата или его геометрического представления необходимо выполнить ряд построений. Давайте подробнее рассмотрим правила сложения и вычитания векторов.
Что такое вектор?
Вектор — это отрезок с направлением.
Вектор и луч часто путают и допускают грубую ошибку. Вектор – это направленный отрезок, а любой отрезок имеет величину, то есть его можно измерить линейкой. Луч имеет начало и направление, но он бесконечен, то есть измерить его невозможно. Так же, как нельзя и складывать лучи между собой или луч с вектором.
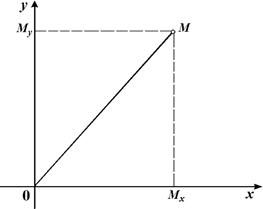
Вектор иногда располагается в декартовой системе координат. Тогда, проведя перпендикуляры к каждой из осей, можно получить проекции вектора на оси Ox и Oy. Каждая из этих проекций будет сегментом. Также, если прямоугольник составлен из проекций, первым вектором будет гипотенуза. Иногда это используется при сложении векторов.
Сложение и вычитание векторов
Есть только два способа и метода добавления векторов. Есть и третий, но он не считается отдельным методом, так как вытекает из первых двух. Но мы рассмотрим его отдельно, чтобы не возникло вопросов при дальнейшем изучении предмета.
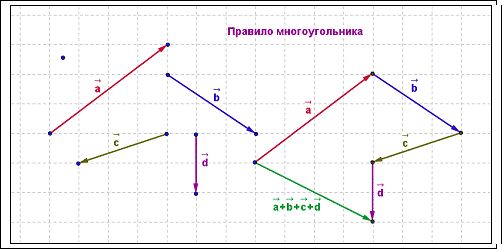
Правило многоугольника
Чтобы добавить векторы с помощью правила многоугольников, при параллельном переносе объедините конец первого вектора с началом второго, конец второго с началом третьего и так далее, пока не закончатся векторы для добавления.
После этого нужно соединить начало первого вектора с концом последнего вектора и указать направление. Результирующий вектор будет направлен в сторону последнего, участвовавшего в сложении.
Таким образом вы можете добавить любое количество векторов. Если таким образом складываются только два вектора, метод называется правилом треугольника
Нужно понять и запомнить, что у отрезка одна определяющая величина: размер. У вектора определяющих величин две: размер и направление. Поэтому нельзя менять направление вектора и его размер. Любые действия нужно осуществлять с помощью параллельного переноса, то есть без изменения направления.
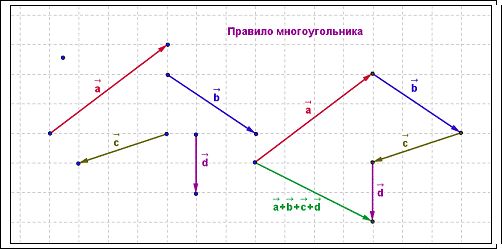
Правило параллелограмма
Правило параллелограмма более сложное; его можно применить только к двум векторам. Если вам необходимо добавить таким способом большее количество векторов, например три, операция выполняется в следующем порядке:
- Сложите любые два вектора, используя правило параллелограмма. В результате получится определенный вектор и у нас остался еще один, не участвовавший в сложении.
- Результирующие и остаточные векторы складываются по тому же правилу.
- Этот процесс можно повторять столько раз, сколько того требуют условия задачи.
Само правило параллелограмма заключается в том, что начала двух векторов совмещаются. После этого полученная фигура достраивается до параллелограмма. Диагональ, исходящая из начала двух векторов, является результатом сложения. Вектор должен быть направлен в противоположном направлении от общего начала двух векторов.
Чтобы вычесть векторы любым способом, направление вычитаемого вектора меняется на противоположное. Полученные векторы добавляются любым методом.
Сложение в декартовой системе
В декартовой системе все векторы раскладываются по проекциям, после чего добавляются отрезки проекций: проекции на ось Ох отдельно, на ось Оу отдельно. После этого из полученных двух проекций снова собирается вектор.
Что мы узнали?
Мы узнали, что такое вектор. Мы рассказали о правилах сложения и вычитания векторов. Мы обсудили, чем вектор отличается от луча и обсудили метод работы с векторами в декартовой системе координат.








Комментирование закрыто