
Пересечение высот треугольника относится к одной из трех примечательных точек треугольника. Эти точки называются замечательными не своей красотой, а своим отношением к золотому сечению треугольника, характеризующему эту фигуру.
Высота
Что такое высота? Высота — это перпендикуляр, падающий из вершины треугольника на прямую, содержащую противоположную сторону треугольника (может оказаться, что высота попадет на продолжение стороны, как это бывает с тупоугольными треугольниками).
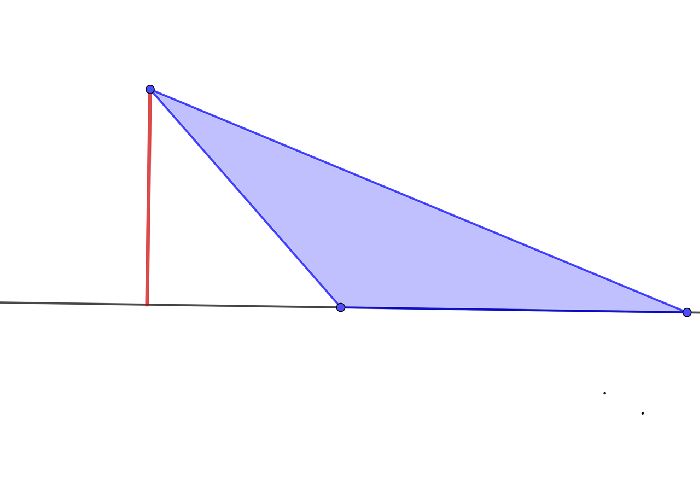
Точка пересечения высот
Любой треугольник имеет три высоты, и они всегда пересекаются в одной точке. Эта точка является одним из трёх центров треугольника и называется ортоцентром.
Еще со времен Древней Греции приставкой «орто» обозначали перпендикуляр. Ортогоналями звались перпендикулярные прямые.
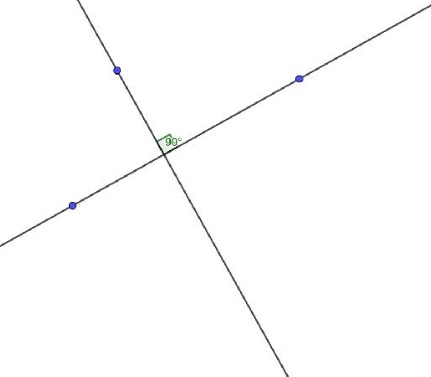
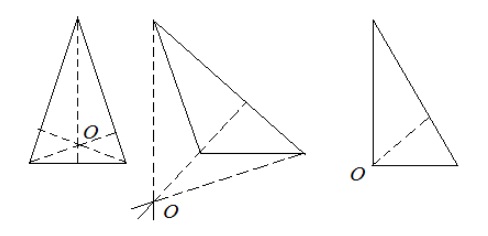
Ортоцентр имеет три варианта размещения в зависимости от типа треугольника:
- Внутри фигуры. В остроугольных треугольниках пересечение высот всегда находится внутри фигуры. Это связано с тем, что все высоты в таком треугольнике внутренние.
- Совпадает с верхом. Этот случай типичен для прямоугольных треугольников. В таких треугольниках две высоты из трёх будут совпадать со сторонами. Если быть точнее, то совпадающие стороны — это ножки. Осталась одна высота, которая будет спускаться сверху под острым углом. Именно эта вершина будет ортоцентром треугольника.
- Не в форме. Внешнее расположение ортоцентра возможно только в тупоугольном треугольнике. Чтобы получить ортоцентр такого треугольника, иногда необходимо продлить высоты до тех пор, пока они не пересекут внешнюю высоту. Почему? Потому что внешняя высота выходит за пределы треугольника и опускается до продолжения одной из сторон, а две внутренние стороны всегда ограничиваются треугольником. Следовательно, без дальнейших построений ортоцентр тупоугольного треугольника найти невозможно.
Золотое сечение треугольника
Золотое сечение треугольника – это маленький треугольник на фигуре, который определяется как пересечение трех центров треугольника.
Три центра треугольника:
- Половина пересечения
- Точка пересечения высот
- Пересечение медиан.
Золотое сечение иногда может вырождаться в прямую линию или даже в точку. В равнобедренном треугольнике пересечение высот и медиан совпадают, в результате для построения золотого сечения понадобится всего 2 точки и золотое сечение выродится в отрезок.
О центрах треугольника существует целая онлайн энциклопедия. Список центров треугольника и свойств каждого из них был начат Карлом Кемберлингом в 1994 году. Онлайн ресурс пополняется все новыми и новыми данными по мере их открытия в высшей математике. В школьном курсе рассматривается только 3 центра треугольника.
В правильном треугольнике каждая высота совпадает с соответствующей медианой, биссектрисой и высотой. Это означает, что все три центра треугольника совпадут, а золотое сечение треугольника будет точкой.
Обратите внимание, что вы не можете создать уравнение пересечения высот треугольника. Можно составить только уравнение прямой. Например, создайте два уравнения высоты, соедините их и найдите координату точки пересечения.
Что мы узнали?
Мы узнали, в каких конструкциях участвует пересечение высот треугольника. Мы рассказали о случаях, когда эта точка совпадает с другими центрами треугольника, и выяснили особенности расположения ортоцентра в разных видах треугольников.








Комментирование закрыто