
Равнобедренный треугольник чаще всего встречается в задачах по геометрии. Так уж получилось, что равнобедренный треугольник решить не так просто, как обычный, но в то же время он обладает рядом интересных свойств, которые могут затруднить решение задачи.
Равнобедренный треугольник
Равнобедренный треугольник – это треугольник, две стороны которого равны друг другу. Тогда третья сторона называется основанием, а равные стороны считаются боковыми.

Любой равнобедренный треугольник обладает рядом свойств:
- Углы при основании равнобедренного треугольника равны.
- Медиана, проведенная к основанию равнобедренного треугольника, — это биссектриса и высота.
Именно эти два свойства определяют специфические свойства равнобедренных треугольников. Как и произвольные треугольники, равнобедренные треугольники бывают 3-х типов:
- Острый угол
- Прямоугольный
- Тупой.
Углы при основании равнобедренного треугольника равны, а сумма углов треугольника всегда равна 180 градусам. Поэтому в равнобедренном и тупоугольном треугольнике наибольший угол всегда лежит напротив основания. Если такой угол лежал бы при основании, то сумма углов превысила бы 180 градусов, а это невозможно.
Тупоугольный треугольник
Тупой угол – это угол больше 90 градусов. Очень часто тупоугольный треугольник стараются изобразить так, чтобы тупой угол находился в основании треугольника. Такой подход облегчает восприятие фигуры.
Тупой угол придает любому треугольнику несколько особенностей:
- Две высоты тупоугольного треугольника будут находиться вне треугольника. Они приходятся на продолжение одной из сторон.
- Ортоцентр, т е точка пересечения высот треугольника, будет располагаться вне треугольника.
- Два других угла треугольника всегда будут острыми.
Равнобедренный тупоугольный треугольник
Равнобедренный треугольник – это треугольник, который с одной стороны содержит тупой угол, а с другой стороны имеет две стороны, равные друг другу.
Такой равнобедренный треугольник сложно воспринимать визуально. Дело в том, что, с одной стороны, учащиеся часто изображают тупоугольные треугольники так, чтобы тупой угол находился в основании.
Но если при основании провести тупой угол, то реальное основание тупоугольного равнобедренного треугольника визуально совпадет со стороной. Такой подход очень часто приводит к ошибкам. Поэтому лучше нарисовать равнобедренный тупоугольный треугольник с тупым углом на противоположной стороне основания, а сам угол отметить непосредственно на чертеже.
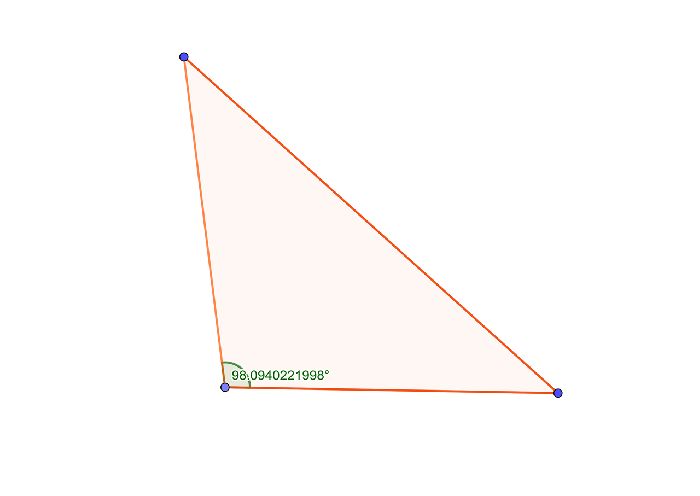
С другой стороны, такой подход не всегда помогает воспринимать фигуру как тупоугольный треугольник. Поэтому необходимо обозначать углы, а при решении задачи доказывать или проверять условие доказательства существования тупого угла в треугольнике.
Что мы узнали?
Мы узнали, что такое тупоугольный равнобедренный треугольник и какие функции он имеет. Мы рассказали о том, как лучше всего нарисовать тупоугольный треугольник, и выделили проблемы, которые могут возникнуть с этой задачей при решении задач.








Комментирование закрыто