
Прямоугольник уникален своей простотой. Опираясь на этот рисунок, ученики начинают изучать основы геометрии. Поэтому они теряются в старших классах, не зная основных свойств и свойств прямоугольника, напрасно считая, что эта фигура слишком проста.
Прямоугольник
Определение прямоугольника известно еще с начальной школы: это параллелограмм, у которого все углы равны 90 градусам. Возникает вопрос: что такое параллелограмм?
Несмотря на сложное название, эта форма проста, как прямоугольник. Параллелограмм – это выпуклый четырехугольник, стороны которого попарно равны и параллельны.
Обязательно выделите в определении слово выпуклый. Потому что в геометрии четко разделены выпуклые и невыпуклые квадраты. Более того, невыпуклые фигуры вообще не изучаются в школьном курсе математики, поскольку они гораздо более непредсказуемы по своим свойствам.
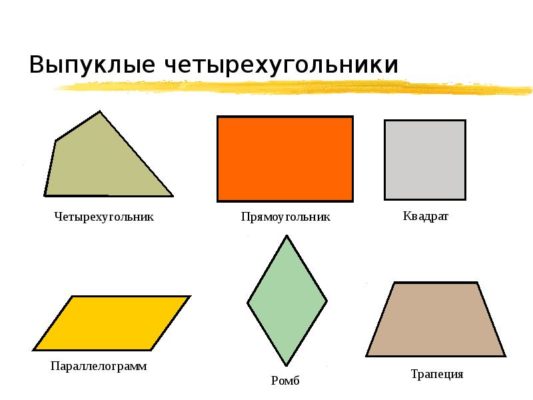
Прямоугольник это частный случай параллелограмма. При этом существуют и другие частные случаи параллелограмма, например, ромб; и еще один особенный частный случай прямоугольника – квадрат. Поэтому перед тем, как доказывать, что фигура является прямоугольником, нужно доказать, что она является параллелограммом.
Свойства прямоугольника
Свойства прямоугольника можно разделить на две группы: свойства параллелограмма и свойства прямоугольника.
Свойства параллелограмма:
- Противоположные стороны равны и попарно параллельны.
- Противолежащие углы равны.
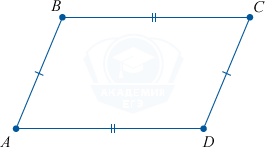
Свойства прямоугольника:
- Все углы равны 90 градусам, как следует из определения фигуры.
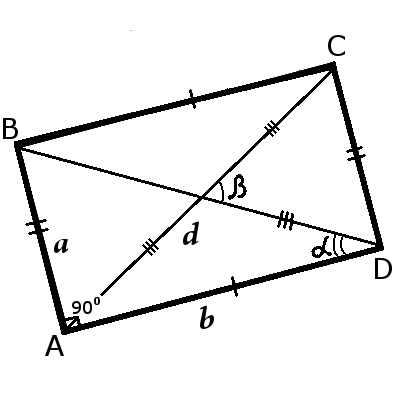
- Диагональ прямоугольника делит фигуру на два небольших равносторонних треугольника. Это свойство легко доказать. Треугольники будут прямоугольными, потому что они включают в себя один угол в 90 градусов. В этом случае диагональ будет общей стороной, а катеты равными, так как противоположные стороны параллелограмма попарно равны и параллельны.
- Диагонали прямоугольника равны.
Признаки прямоугольника
Прямоугольник имеет только три основных признака:
- В углу. Если один из углов параллелограмма равен 90 градусов, то параллелограмм является прямоугольником.
- Если три угла четырёхугольника равны 90 градусам, то четырёхугольник является прямоугольником. Заметим, что в этом случае не нужно доказывать, что перед нами параллелограмм. Достаточно знать значения углов квадрата.
- По диагоналям: если диагонали параллелограмма равны, то такой параллелограмм является прямоугольником.
Обратите внимание на то, к какой фигуре применяется функция, это важно в доказательстве.
В чем разница признака и свойства? Признак это отличие по которому можно выделить фигуру среди других. Как имя у человека. Вы видите знакомого, вспоминаете его имя и сразу знаете, что от него ожидать. А вот ожидания от человека это уже свойства. Свойства можно применять только после того, как вы доказали, что перед вами та или иная фигура. А для этого доказательства нам и необходимы признаки.
Что мы узнали?
Мы узнали, что такое параллелограмм. Мы рассказали о частных случаях параллелограмма, в том числе о самом распространенном – прямоугольнике. Выявлены свойства и характеристики прямоугольника. Мы заметили, что часть знаков справедлива для всех квадратов, а часть — только для параллелограмма.








Комментирование закрыто