
Свойства параллельных прямых чрезвычайно распространены при решении задач и доказательстве теорем. Произвольные прямые встречаются редко, но встречаются фигуры типа квадрата или параллелограмма, где параллельные прямые могут стать основой задачи, а без знания свойств параллельных прямых решить такие задачи невозможно.
Что такое свойства параллельных прямых
Для начала выделим определения, которые необходимо знать для изучения свойств параллельных прямых.
Параллельными называют линии, не имеющие общих точек, или линии, не пересекающиеся друг с другом и лежащие в одной плоскости.
Пересечение означает, что у двух объектов есть общая точка или набор точек. Поэтому когда в геометрии говорят, что прямые имеют общую точку, имеется в виду, что они пересекаются.
При пересечении двух прямых поперечных образуются перекрестно лежащие, соответствующие и односторонние углы.
Это аксиома параллельных прямых, которая чрезвычайно важна при доказательстве некоторых свойств и является основным свойством параллельных прямых. Аксиома гласит, что через точку на плоскости можно провести только одну прямую, параллельную данной.
Две группы свойств параллельных прямых
Свойств параллельных прямых всего 5, но они разделены на две большие группы: следствия из аксиомы параллельных прямых и следствия из свойств параллельных прямых. Начнем с первой группы.
Следствия из аксиомы параллельных прямых
Следствие 1
Если одна из двух параллельных прямых параллельна третьей, то и другая параллельна ей.
Кажется, это логично и не требует доказательств. Но в геометрии число утверждений, не требующих обоснования, крайне мало, и каждое из них называется аксиомой.
Аксиомы были выведены еще на заре геометрии и с тех пор мало что изменилось. Большая часть современных теорем выведена на основании аксиом Древней Греции. Эти утверждения единственные, что в математике не требует доказательства.
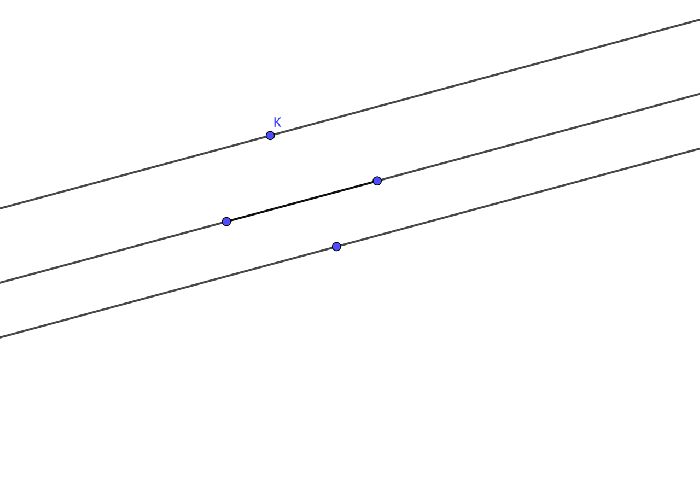
Проведем две параллельные прямые а и б. Линия с параллельна прямой а. Предположим, что с не параллельна прямой b. Тогда она должна иметь какое-то пересечение К. То есть две прямые с и b проходят через точка К. При этом каждая из этих прямых должна быть параллельна линии а.
То есть через одну точку плоскости проводятся две прямые, параллельные данной. Это невозможно, поскольку противоречит аксиоме параллельных прямых. Это означает, что исходное предположение было неверным и прямые c и b параллельны.
Следствие 2
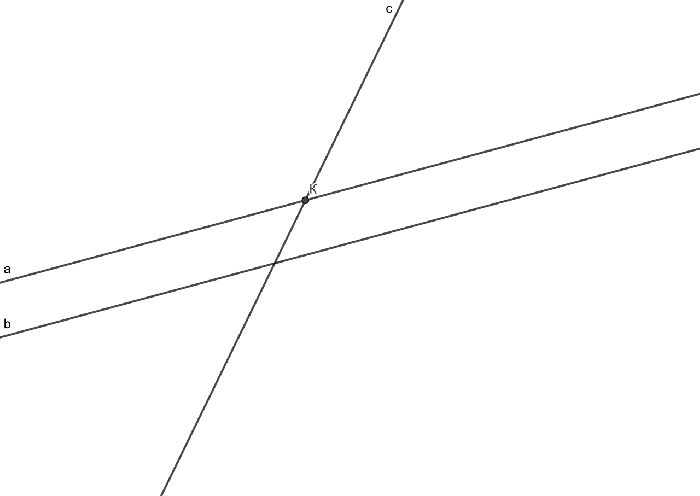
Следствие 2 очень важно, поскольку оно говорит о секущей двух параллельных прямых. Свойство гласит: если линия пересекает одну из параллельных прямых, она также пересечет и другую.
Доказательство также проводится методом внутреннего противоречия. Проведем две прямые: а и б. Представим, что линия с пересекает линию а, но не пересекает линию б. Тогда прямые с и б параллельны. Также пересекаются приблиз., то есть эти прямые имеют общую точку К.
Тогда через точку К проходят прямая а и прямая с, но каждая из них параллельна b. Это означает, что через одну точку проходят две прямые, параллельные прямой b, а это невозможно по аксиоме параллельных прямых. Это означает, что исходное предположение было неверным и линия c пересекает каждую из линий a и b, что и нужно было доказать.
Следствия из признаков параллельности
Эту группу легче всего запомнить. Есть всего 3 свойства параллельности прямых, и каждое из них имеет свое следствие.
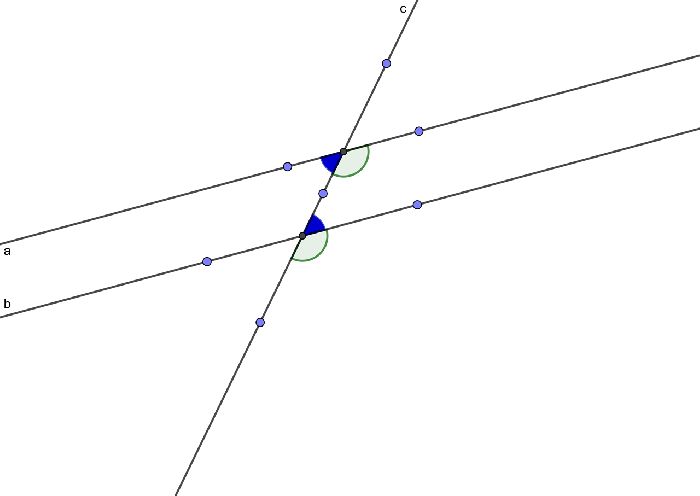
- Линии параллельны, если углы их пересечения на поперечной стороне равны. Следствие вполне логичное: углы пересечения двух параллельных прямых и поперечной равны.
- Прямые параллельны, если соответствующие углы равны. Следствие: соответствующие углы параллельных прямых и трансверсали равны.
- Прямые параллельны, если сумма односторонних углов равна 180. Соединение: сумма односторонних углов для параллельных прямых и трансверсали равна 180
Что мы узнали?
Мы дали понятие о параллельных прямых, выделили две большие группы свойств параллельных прямых и доказали два свойства. Мы узнали, как использовать аксиому параллельных прямых при доказательстве теорем геометрии.








Комментирование закрыто