Сумма углов прямоугольного треугольника

Сумма углов треугольника – устойчивая величина. Но прямоугольный треугольник выделяется среди других набором специфических характеристик. Сумма углов не является исключением, поэтому стоит поговорить об этом свойстве прямоугольных треугольников, чтобы в дальнейших исследованиях не возникло вопросов.

Треугольник

Несмотря на свою обособленность от других фигур, треугольник представляет собой такой же многоугольник, как прямоугольник, квадрат или ромб. Разница лишь в количестве углов. Это формула, определяющая сумму углов многоугольника в зависимости от количества сторон; мы поговорим об этом чуть позже.

Итак, треугольник – это фигура, имеющая три стороны и три угла. Традиционно одну из сторон считают основанием, а две другие называют боковыми. Обозначение не является основным, поэтому за условное основание принимается любая из сторон треугольника. Это обозначение необходимо лишь для облегчения понимания чертежа.

Сумма углов треугольника

Существует два варианта нахождения общей суммы углов треугольника:

• Математический анализ. За такими страшными словами скрывается обычная простая формула:

180*(n-2) – где n – количество сторон многоугольника.

• Второй метод – геометрический. Именно таким образом впервые было выведено утверждение, что сумма углов в треугольнике равна 180 градусам. Давайте посмотрим на это поближе.

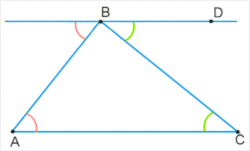
Пусть треугольник ABC — любой треугольник с основанием AC. Далее построим линию ВD, проходящую через точку В, параллельно основанию. Тогда мы получим две параллельные прямые: AC и ВD с двумя секущими AB и BC.

Будем считать углы секущими. Сумма трех углов при вершине В будет равна 180 градусам, так как они представляют собой прямой угол. Тогда внутренние углы треугольника будут равны внешним углам, лежащим поперек треугольника. То есть сумма углов треугольника равна градусной мере развернутого угла и равна 180 градусам.

Важно понимать, что внешние углы нельзя назвать внешними углами треугольника, так как внешние углы получаются продолжением одной из сторон треугольника, а прямая BD не является продолжением стороны треугольника.

Прямоугольный треугольник

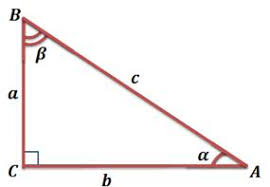
Прямоугольный треугольник содержит угол 90 градусов. Этот угол называется прямым, отсюда и название фигуры. Чему равна сумма углов прямоугольного треугольника? Такой же, как и во всех остальных треугольниках – 180 градусов. Однако если один из углов определен и равен 90 градусам, то сумму остальных двух можно определить:

180-90=90 – то есть сумма косых углов прямоугольного треугольника равна 90 градусов.

Но косые углы – это нематематическое определение. Может ли прямоугольный треугольник иметь еще один прямой угол? Если бы такой угол мог существовать, он был бы равен 90 градусам. То есть оставшийся третий угол:

90-90=0 – и третий угол в этом случае будет равен нулю, что невозможно. Точно так же, как в прямоугольном треугольнике невозможно существование тупого угла. Потому что тупой угол всегда больше 90 градусов.

Это значит, что можно сделать вывод, что в прямоугольном треугольнике сумма острых углов равна 90 градусов.