
Параллельные линии повсюду в нашей жизни. Они являются основой симметрии, которая так или иначе присутствует в каждом элементе мебели, архитектуры и инструментах труда. Знание определения и свойств параллельных прямых помогает не только при решении задач по математике 6 класса, но и при расчете реальных бытовых предметов.
Что такое параллельные прямые
Параллельными прямыми называются линии, которые не пересекаются.
В этом определении параллельных прямых есть небольшая неточность: прямые, которые имеют больше одной общей точки, совпадают. Иногда о них также говорят, как о параллельных.
Прямая, пересекающая параллельные прямые, называется секущей. При пересечении устройств 8 углов. Друг онлайн они могут быть соотвественными, ондостронными и крестолежащими. Давайте посмотрим на них, например.
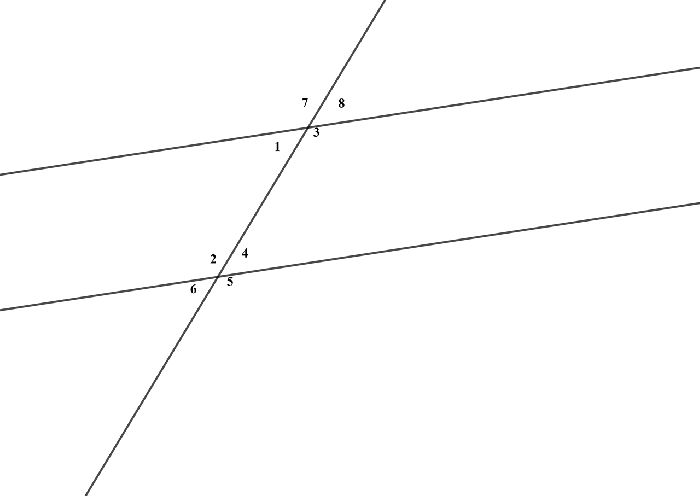
- Соответствующие углы: 7 и 2, 1 и 6, 8 и 4, 3 и 5
- Рядом друг с другом: 7 и 5, 8 и 6, 1 и 4, 3 и 2
- Односторонние: 1 и 2, 3 и 4, 7 и 6, 8 и 5
Аксиома параллельных прямых
Аксиома параллельных прямых — одно из основных положений геометрии. Через точку можно провести прямую, параллельную этой, и при этом только одну – это самая распространенная формулировка аксиомы.
Из аксиомы следуют два следствия:
- Если прямая параллельна одной из двух параллельных прямых, то она параллельна второй.
- Если прямая пересекает одну из параллельных прямых, то она пересекает и вторую.
Обратите внимание, что аксиома справедлива только для плоскостности. В пространстве может быть вариант, когда прямая параллельна плоскости, в котором будет бесконечное множество параллельных линий, проходящих через одну точку. Значит, на странице это состояние не является программой изображения.
Расстояние между параллельными прямыми в любой точке будет одинаковым и равным величине отрезка, перпендикулярного каждой из прямых.
Фигуры с параллельными прямыми
Существует множество фигур, в построении которых используются параллельные прямые линии. Например, параллелограмм состоит из двух пар параллельных отрезков.
Квадрат и прямоугольник также состоят из попарно параллельных прямых, но в то же время являются частным случаем параллелограмма.
В треугольнике средняя линия всегда параллельна основанию.
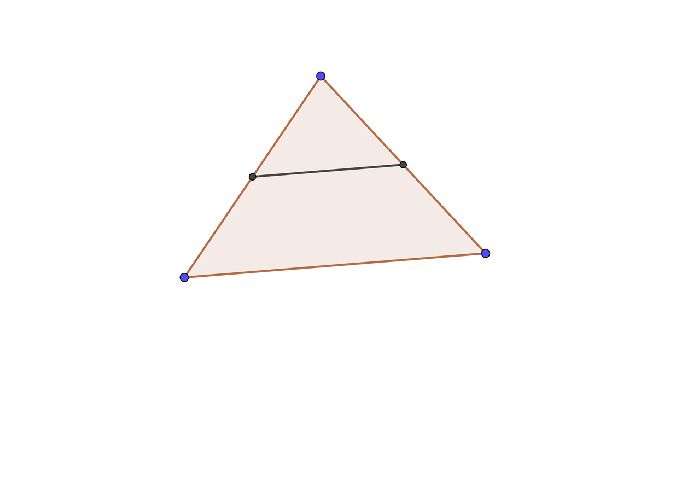
Инжир. 2. Средняя линия треугольника.
Есть еще одна интересная фигура: трапеция. В трапеции большое и малое основания параллельны друг другу, а боковые стороны не параллельны.
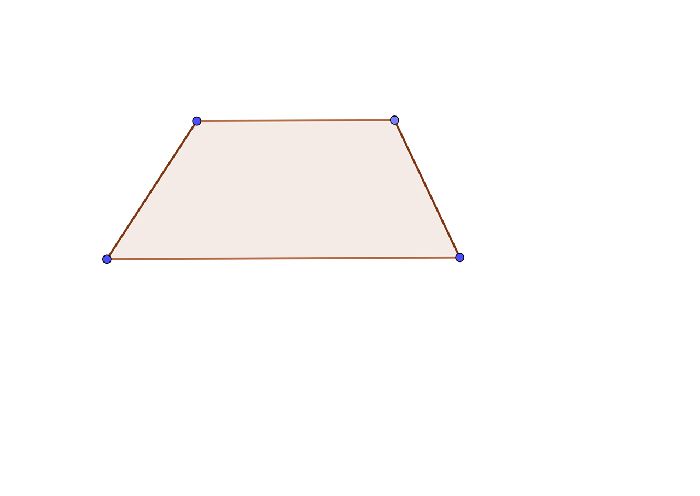
Если прямые непараллельны, то они пересекаются, но если не параллельны отрезки, это вовсе не значит, что они пересекутся. Отрезки имеют конечное значение длинны, а поэтому могут просто стоять отдельно друг от друга. При этом, отдельных видов или каких-либо таблиц параллельных прямых нет, и вряд ли они когда-нибудь появятся.
Что мы узнали?
Мы узнали все о параллельных прямых, вывели аксиому параллельных прямых и следствия из нее. Они рассказали о разнице понятий о параллельных прямых и параллельных отрезках, а также выяснили, почему аксиома о параллельных прямых работает только на плоскости. Привели формы фигур, для простения хорошо програмированные праймые.








Комментирование закрыто