
Подобные треугольники – следующий шаг в изучении треугольников по подобию. Необходимо полностью понимать возможности подобия треугольников, чтобы правильно использовать все свойства для решения задач. Давайте разберемся в различиях между равенством, подобием и эквивалентностью, а также поговорим о свойствах сторон и определим площади подобных треугольников.
Подобные треугольники
Подобные треугольники – это треугольники, соответствующие стороны которых пропорциональны и имеют равные углы. Подобные треугольники также подобны с коэффициентом подобия 1.
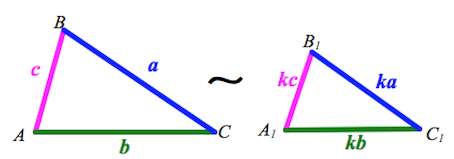
Коэффициент пропорциональности (подобия) – это отношение длин сторон одного треугольника к соответствующим длинам сторон другого треугольника. Важно при подсчете коэффициента строго соблюдать какая сторона к какой относится.
Например, если вы начали расчет с деления сторон большего треугольника на стороны меньшего, вам следует продолжать следовать этому подходу.
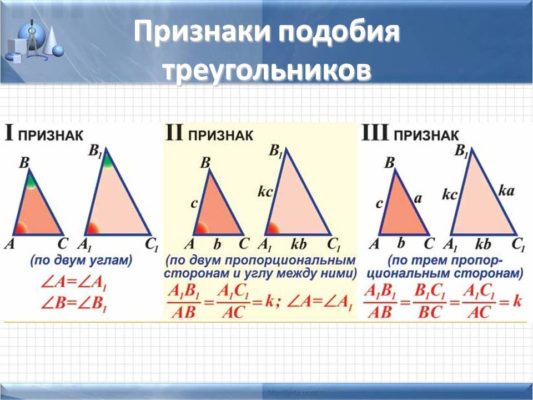
Признаки подобия
Знаки равенства чем-то похожи на знаки равенства в треугольниках. Всего их три:
- На двух углах. Если два угла треугольника равны соответствующим углам другого треугольника, то такие треугольники подобны.
- На трёх страницах. Если три стороны треугольника пропорциональны соответствующим сторонам другого треугольника, то такие треугольники подобны.
- О двух сторонах и угле между ними. Если две стороны треугольника пропорциональны двум сторонам другого треугольника, а углы между этими сторонами равны, то такие треугольники подобны.
Свойства подобных треугольников
- Стороны подобных треугольников пропорциональны и относятся друг к другу в соотношении, равном коэффициенту подобия.
- Углы подобных треугольников равны.
- Площади подобных треугольников относятся друг к другу в соотношении, равном квадрату коэффициента подобия.
Давайте подробнее рассмотрим новейшую недвижимость. Почему все стороны относятся как коэффициент к первой степени, а площади возводятся в квадрат? Потому что площадь равна половине произведения основания на высоту.
Пропорциональны друг другу не только стороны, но и характерные отрезки: медианы, высоты, биссектрисы.
Получается, что обе части произведения площади пропорциональны, но в произведении участвуют и высота, и основание. Это означает, что коэффициент пропорциональности необходимо возвести в квадрат.
$$S_1={1\over{2}}*h_1*a_1$
$$S_2={1\over{2}}*t_2*a_2$
$${S_1\over{S_2}}={{h_1*a_1}\over{h_2*a_2}}$
$${S_1\over{S_2}}={h_1\over{h_2}} *{a_1\over{a_2}}$
$${S_1\over{S_2}}=k *k$
$${S_1\over{S_2}}=k ^2$
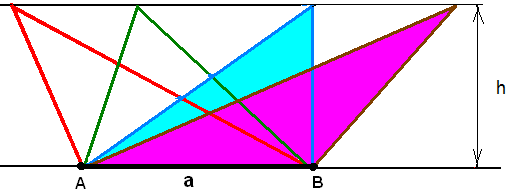
Нужно четко различать понятие подобных и равновеликих треугольников. Подобные треугольники имеют коэффициент подобия, в соответствие с которым соотносятся стороны треугольника. А равновеликие треугольники могут, как угодно разнится по значениям сторон, важно лишь, чтобы площади треугольников были равны.
Что мы узнали?
Мы узнали, что такое подобные треугольники, и рассказали об их свойствах. Мы рассказали о связи площадей подобных треугольников и вывели эту зависимость на практике для лучшего запоминания формулы.








Комментирование закрыто