
Многоугольник, имеющий три вершины и три стороны, называется треугольником. Треугольник называется равносторонним или правильным, если все три стороны равны и все три угла равны 60°. О методах расчета площади равностороннего треугольника мы поговорим в этой статье.
Определение
Правильный треугольник – это часть плоскости, ограниченная тремя одинаковыми отрезками. Они соединены точками, не принадлежащими одной прямой. Здесь все три угла равны и равны 60 градусам. Поэтому для определения площади правильного треугольника можно воспользоваться упрощенными формулами.
Равносторонний треугольник является частным случаем равнобедренного треугольника.
Площадь правильного треугольника вычисляется путем подстановки параметров фигуры в классическую формулу.
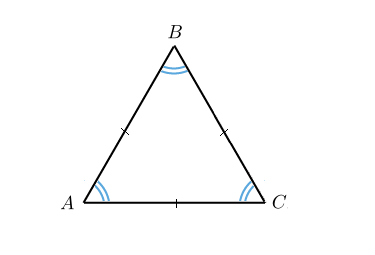
Нахождение площади правильного треугольника
- Первая формула площади правильного треугольника является стандартной. Площадь равна половине произведения основания на высоту: $S= {1\over2}h*a$.
- Существует формула нахождения площади стороны, вытекающая из первой, но характерная только для правильных треугольников. В правильном треугольнике ABC нарисуем высоту AM, которая также будет медианой и биссектрисой.
Это свойство характерно для равнобедренных треугольников, но любой правильный треугольник и будет равнобедренным, просто любая из его сторон может считаться основанием, так как две другие стороны в любом случае будут равны.
В результате треугольник разделился на два равных прямоугольных треугольника. Теперь найдем значение высоты, заменим его классической формулой площади треугольника и получим формулу равностороннего треугольника.
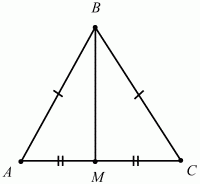
В прямоугольном треугольнике АВМ катет АМ можно выразить через синус угла АВМ. Этот угол известен и равен 60 градусам, а значит, известны и значения синуса и косинуса этого угла. Поскольку АМ – противоположность, а значит, для его нахождения нужно воспользоваться формулой синуса.
$$Sin(ABM)={AM\над AB}$
С другой стороны, синус 60 градусов известен заранее и равен $$\sqrt{3} \over 2$$ . Это означает, что мы можем выразить значение АМ:
$$AM=AB*sin(ABM)=AB* {\sqrt{3}\over 2}$
Все стороны треугольника равны между собой, поэтому для простоты обозначим их буквой а.
AB=AC=BC=а
Тогда формула будет выглядеть так:
$$AM=a*{\sqrt{3}\over2}$
Теперь вспомним классическую формулу площади треугольника:
$S= {1\over2}h*a$, где a — основание треугольника, h — высота, проведенная к этому основанию. Формула площади равностороннего треугольника будет выглядеть так:
$$S={1\over2}*BC*AM={1\over2}*a*a*{\sqrt{3}\over2}=a^2*{\sqrt{3}\over4}$
BC заменили на a, так как все стороны равны между собой, а значение высоты мы нашли ранее. Полученная формула значительно проще классических по количеству требуемых параметров. Чтобы найти площадь правильного треугольника, достаточно знать значение одной из сторон. Это возможно из-за подобия углов такого треугольника.
Только в правильном треугольнике возможно нахождение площади через сторону.
По этой же причине нельзя использовать эту формулу для равнобедренного или произвольного треугольника. Прежде чем использовать эту формулу, необходимо доказать, что треугольник правильный, или убедиться, что это условие задано в исходных данных задачи.
Что мы узнали?
Площадь правильного треугольника можно вычислить через сторону, поскольку речь идет о фигуре с теми же параметрами, или через высоту по классической формуле. Здесь углы также будут одинаковыми. При решении некоторых задач по геометрии стоит помнить, что высоты данной плоской фигуры, ограниченной тремя сторонами, равны между собой.








Комментирование закрыто