
В 7 классе по математике изучаются разные виды треугольников, в том числе равнобедренные. Равнобедренный треугольник — это треугольник, у которого две равные стороны называются боковыми, а третья сторона называется основанием: в равнобедренном треугольнике углы при основании равны. Какова площадь равнобедренного треугольника, по какой формуле следует производить расчеты – об этом мы поговорим в статье.
Определение
Треугольник – это фигура, состоящая из трех точек, соединенных друг с другом. Элементами треугольника являются три стороны и три угла. Сумма углов в треугольнике всегда равна 180 градусов.
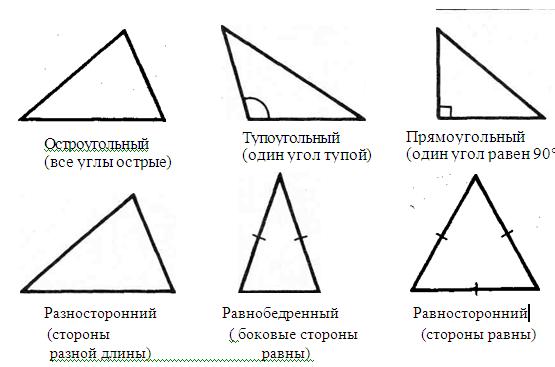
Треугольник может быть:
- Равнобедренный, если две стороны треугольника равны.
- Равносторонний, если все стороны треугольника равны между собой и каждый угол равен 60 градусам.
- Прямоугольный, если он содержит прямой угол.
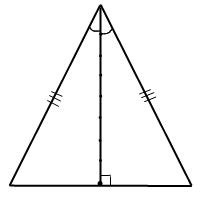
В равнобедренном треугольнике медиана, проведенная к основанию, совпадает с основанием и высотой. Именно это свойство мы и будем использовать при нахождении специализированной формулы площади равнобедренного треугольника.
Формула площади равнобедренного треугольника
Выведем формулу площади равнобедренного треугольника. Существует два варианта равнобедренного треугольника: через сторону и основание или по классической формуле.
Классическая формула – самый простой вариант. Площадь любого треугольника равна половине произведения основания на высоту. И равнобедренный треугольник не является исключением:
$S={1\over{2}}*a*h$, где a — основание треугольника, а h — высота, проведенная к этому основанию.
Это формула через сторону и основание. Чтобы показать это, рассмотрим рисунок.
Обозначим высоту через h, сторону через a и основание через b. Тогда высоту можно найти как сторону полученного прямоугольного треугольника по теореме Пифагора:
$$h=\sqrt{a^2-{b\over{2}}*в}$
Подставляем полученную формулу вместо высоты и получаем специальную формулу равнобедренного треугольника:
$$S={1\over{2}}*a*{\sqrt{a^2-{b\over{2}}*в}} $
Площадь можно найти через угол как половину произведения синуса угла между сторонами и этими сторонами.
Подобный способ, когда равнобедренный треугольник рассматривают, не как целую фигуру, а как два равных между собой прямоугольных треугольника, часто используют для вычислений. Эти треугольники получаются в результате проведения высоты к основанию равнобедренного треугольника. Важно понимать, что в равнобедренном треугольнике только высота, проведенная к основанию, имеет специфические свойства.
Что мы узнали?
Из статьи мы узнали, что площадь любого треугольника можно легко найти, подставив в формулу значение высоты и основания, до которого эта высота была опущена. Однако необходимо учитывать тип треугольника. Для равнобедренных, равносторонних и прямоугольных треугольников вы можете упростить нахождение площади, используя конкретные треугольники.








Комментирование закрыто