
В 7 классе изучают разные виды треугольников. Сегодня мы научимся измерять площадь прямоугольного треугольника, а также общие свойства этой фигуры.
Определение понятия
Известно, что треугольник состоит из трёх точек и равного количества отрезков. Тогда часть плоскости, ограниченная этими линиями, будет площадью рассматриваемой фигуры.
В общем случае для нахождения числовых свойств плоской фигуры используются такие параметры, как значения сторон и углов. Иногда нужно создать дополнительные конструкции.
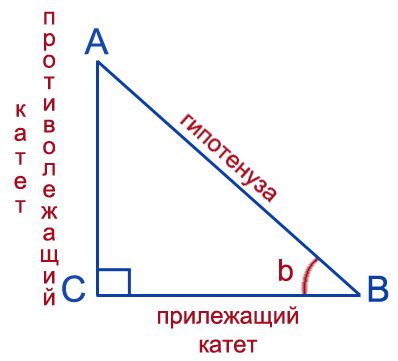
Проще всего определить площадь прямоугольного треугольника через катеты. Но это не всегда возможно, поэтому иногда приходится пользоваться другими формулами.
Характеристики понятия
В прямоугольном треугольнике один из углов равен 90 градусов. Поэтому, когда вы находите площадь, вам обычно не нужно находить высоту; две из трех высот треугольника совпадают с катетами.
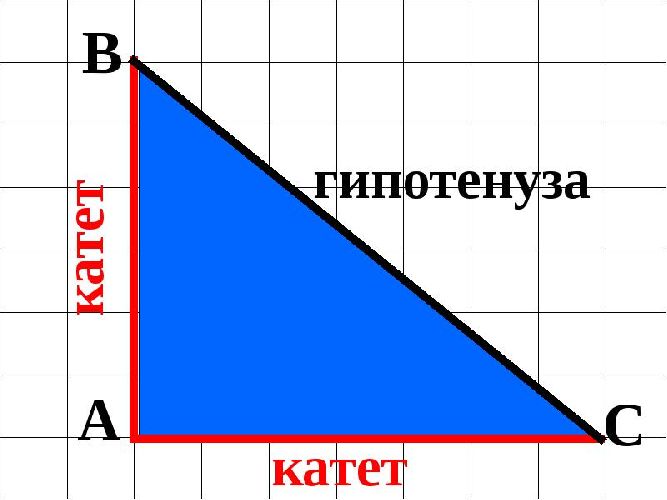
Достаточно найти произведение числовых значений катетов этой геометрической фигуры, а затем разделить результат на два. Таким образом мы получаем общую формулу определения площади прямоугольного треугольника через катеты:
$S=AB∙AC$ где
$AB$, $AC$ — катеты прямоугольного треугольника.
Частные случаи
Чтобы получить правильный результат при определении площади прямоугольного треугольника, можно воспользоваться и другими формулами.
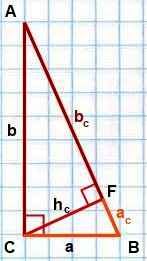
Значит площадь прямоугольного треугольника можно найти через гипотенузу и катет, используя острый угол между ними:
$$S=a*c*sin(a;c)$
Эту формулу еще называют формулой через гипотенузу и катет. В дополнение к этому можно использовать любую формулу, применимую к любому треугольнику.
Решение задач
Для нахождения площади прямоугольного треугольника могут потребоваться дополнительные построения. В некоторых случаях нужно вычесть высоту гипотенузы, чтобы получить высоту или два пропорциональных отрезка.
Хотя бывают проблемы, где указаны числовые значения отрезков, соединяющих верх и основание. Это может быть медиана или биссектриса. Конечно, лучше упростить задачу, используя простые формулы, в зависимости от желаемого результата.
Любую геометрическую фигуру можно разбить на треугольники. Следовательно, используя формулу площади треугольника, можно найти площадь сложной фигуры.
Площадь прямоугольного треугольника можно находить, пользуясь формулой Герона, радиусом вписанной или описанной окружности.
Что мы узнали?
Площадь произвольного треугольника обычно является числовой характеристикой плоской геометрической фигуры. Определить площадь можно несколькими способами, воспользовавшись соответствующими формулами. Но когда мы говорим о прямоугольном треугольнике, задача упрощается, поскольку две из трех высот треугольника совпадают с катетами. Поэтому достаточно подставить в формулу значения ног.








Комментирование закрыто