
Площадь прямоугольного треугольника можно найти несколькими способами. Прямой угол в любой фигуре придает ей свойства, которые можно использовать для правильного и быстрого решения задач.
Прямоугольный треугольник
Для начала давайте обсудим сам прямоугольный треугольник, его функции и свойства. Прямоугольный треугольник – это треугольник, содержащий угол.
Прямоугольный треугольник не может быть тупоугольным, потому что тогда сумма углов треугольника превысит 180 градусов, а это невозможно.
В прямоугольном треугольнике две высоты из трёх совпадают со сторонами — катетами. По этой же причине пересечение высот прямоугольного треугольника совпадает с вершиной под прямым углом.
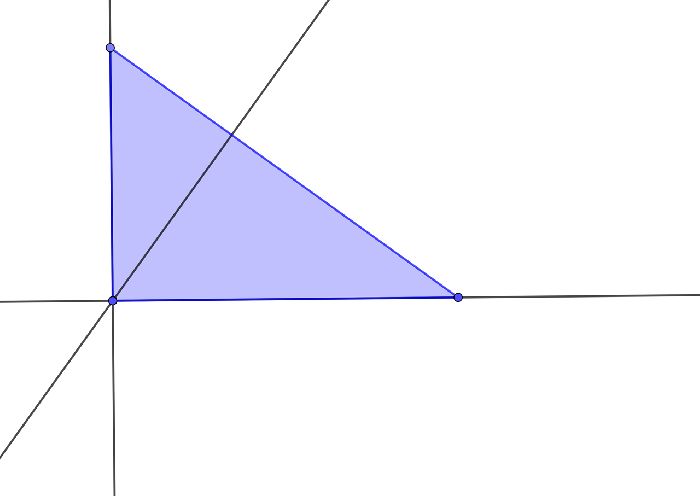
Эта же точка будет центром описанной окружности.
Площадь треугольника
Площадь треугольника обычно находят по стандартной формуле, как половину произведения основания на высоту, проведенную к этому основанию.
$$S={1\over2}*a*h$
Площадь можно найти как половину произведения сторон на синус угла между ними:
$$S={1\over2}*a*b*sin(g)$
Существуют сложные формулы нахождения площади, но они используются крайне редко.
Площадь прямоугольного треугольника
Площадь прямоугольного треугольника находится по тем же формулам, но в некоторых случаях эти формулы можно упростить.
Например, можно воспользоваться тем, что высоты прямоугольного треугольника совпадают с катетами. Тогда стандартная формула будет выглядеть так:
$S={1\over2}*a*b$, где a и b — катеты прямоугольного треугольника.
Это одна из простейших формул площади прямоугольного треугольника. Попробуем преобразовать вторую формулу.
$$S={1\over2}*a*b*sin(g)$
Если вспомнить, что синус угла – это отношение противоположной стороны к гипотенузе. В нашем случае противоположный катет мы обозначим буквой f, потому что а — прилежащий катет, а острый угол можно образовать только между катетом и гипотенузой. Итак, b — гипотенуза.
$S={1\over2}*a*b*sin(g)= {1\over2}*a*b*{f\over{b}}={1\over2}a*f$ — всё получается та же формула.
Значит, первый вывод мы выполнили правильно, а у прямоугольного треугольника есть только одна специальная формула для нахождения площади. Если это не сработает, вы можете использовать общие формулы. Это два возможных способа расчета площади.
Например, если по условиям задачи известна гипотенуза, можно попытаться найти высоту, падающую на гипотенузу, и определить площадь по общей формуле. По такому же принципу можно найти площадь через синус, если известны гипотенуза и катет.
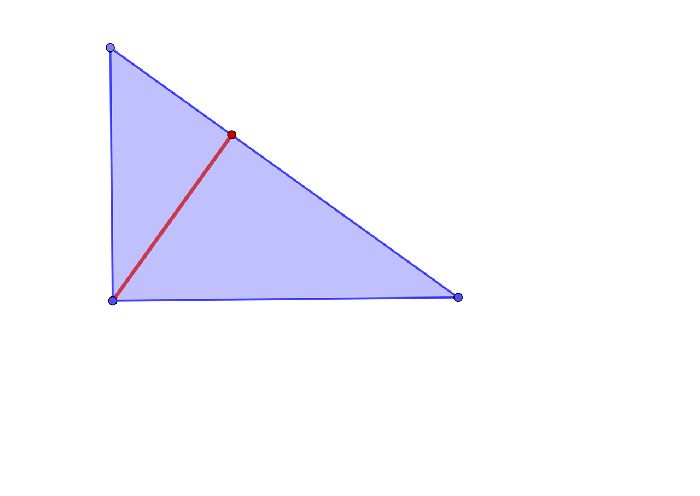
Самое главное помнить, что любая проблема всегда имеет 3 решения и решайте каждое наиболее практичным способом.
Что мы узнали?
Мы поговорили о прямоугольных треугольниках и вывели формулу площади прямоугольного треугольника с помощью катетов. Мы обсудили общие формулы площади треугольников и сказали, что каждая из этих формул подойдет для решения прямоугольного треугольника.








Комментирование закрыто