
Прямоугольный треугольник отличается от произвольного целого числа параметров. В этом смысл стороны, которую можно вычислить по теореме Пифагора; возможность непосредственно использовать тригонометрические функции и несколько конкретных формул, предназначенных для расчета площади прямоугольных треугольников. Именно об этих формулах и пойдет речь в данной статье.
Формула площади прямоугольного треугольника
В классическом случае площадь треугольника находится как половина произведения стороны высоты, приведённой к этой стороне.
В прямоугольном треугольнике у двух сторон из трех высота и сами стороны совпадают рассмотрим природу.
Дан рекладный треугольник АВС с прямым углом на вершине В. Для катеты ВС высота будет катет АВ, а для катеты АВ высота строна ВС. Только гипотенуза нуждается в дополнительных построениях для нахождения высоты.
Именно из этих особенностей и следует формула площади прямоугольного треугольника.
$S= {1\over2}a*b$ где a и b это катеты треугольника. Вот смысл двух сторон, просто подставленных в классическую формулу. В результате получается простейшая формула нахождения площади прямоугольного треугольника ечасть неклассического состояния, когда мнежно катетов неизвестно.
Если в задаче о прямоугольном треугольнике дается значение высоты, то имеется в виду перпендикуляр, проведенный к гипотенузе.
Задача
- В прямоугольном треугольнике высота равна 8, а острый угол при гипотенузе равен 60 градусам. Найдите квадрат прямоугольного треугольника.
Для каждой геометрической задачи существует, как минимум 3 решения.
Конкретно в нашем случае можно выделить два простых метода:
- Найдите гипотенузу и определите площадь квадрата по классической формуле.
- Найдите качество катетов и найдите площадь через катеты.
Мы рассматриваем каждый из вариантов, чтобы иметь представление о возможных путях решения подобных задач.
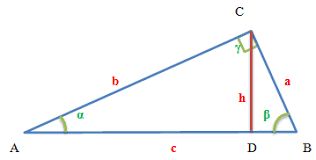
Обозначает треугольник АВС, продем высоту ВН. Угол АСВ равен 60 градусам. Найдем гипотенузу. Он состоит из двух сегментов АН и НС. Найдем чайдж из отрезков, заглом их и получим иское межжное.
АН находим из прямоугольного треугольника АНВ с прямым углом при вершине Н. Сумма острых углов прямоугольного треугольника всегда равна 90 градусам. Значит Угол ВАС=90-60=30.
Используем тригонометрическую функцию. Используем значение тангенса:
$$tg(BAC)= {BH\over AH}=\sqrt{3}$$ – значение тангенса можно взять из таблицы Брадиса или запомнить для трех характерных углов 30, 45 и 60 градусов.
$$АН={ВН\over\sqrt{3}}= {8\over\sqrt{3}}=4,62$
Полученный результат округляем до сотых. Не бойтесь полученных в результате длинных дробных значений. В расчетах они встречаются постоянно, нужно только правильно округлить полученные значения.
По аналогичной схеме вычисляем НС из прямоугольного треугольника ВНС.
$$tg(НСВ)={ВН \over НС}={1 \over \sqrt{3}}$
$$HC={BH\over tg(HCB)}={BH\over{1\over\sqrt{3}}}=BH*\sqrt{3}=8*\sqrt{3}=13.87$
Значение снова округлим до сотых. Складываем два полученных значения вместе и вычисляем значение площади.
АС=АН+НС=4,62+13,87=18,49
$$S={1\over2}*BH*AC={1\over2}*8*18.49=73.96$
Принимаем решения через катеты и собираем результаты.
В прямоугольном треугольнике сторона ВС является гипотенузой. Используем значение синуса:
$$sin(ACB)={BH\over BC}={\sqrt{3}\over2}$
Значение синуса для угла 60 градусов представляет собой табличное значение.
$$BC=BH/sin(ACB)=8/(\sqrt{3}/2)=16/\sqrt{3}=9,23$
Аналогичным методом определяем значение второго катета треугольника АНВ:
$$sin(BAH)=BH/AB=1/2$
$$AB=BH/(1/2)=BH*2=16$
Оба катета найдены, можно изменить программу производитель:
$$S=1/2*AB*BC=1/2*16*9,23=73,84$
Полученные значения схожи. Разница в сотых долях легко объясняется округлениями, которые были произведены для удобства расчета. В подобных расчетах допустимой считается разница в единицах.
Что мы узнали?
Мы тщательно разобрали формулу нахождения площади прямоугольного треугольника. Показали другие варианты нахождения площади, подробно разобрали различные способы решения задач на нахождение площади прямоугольного треугольника.








Комментирование закрыто