
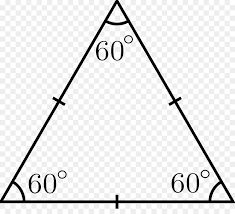
Правильные треугольники — особое явление в геометрии. Все углы в треугольнике точно определены значением 60 градусов. Благодаря этому, помимо обычных способов нахождения площади треугольников, существуют и способы нахождения площади правильного треугольника, не характерные для других фигур. Все способы будут рассмотрены в этой статье.
Формулы для нахождения площади треугольника.
- Первая формула площади правильного треугольника является стандартной. Площадь равна половине произведения основания на высоту: $S= {1\over2}h*a$.
- Существует формула нахождения площади стороны, вытекающая из первой, но характерная только для правильных треугольников. В правильном треугольнике ABC нарисуем высоту AM, которая также будет медианой и биссектрисой.
Это свойство характерно для равнобедренных треугольников, но любой правильный треугольник и будет равнобедренным, просто любая из его сторон может считаться основанием, так как две другие стороны в любом случае будут равны.
В результате треугольник разделился на два равных прямоугольных треугольника. Теперь найдем значение высоты, заменим его классической формулой площади треугольника и получим формулу равностороннего треугольника.
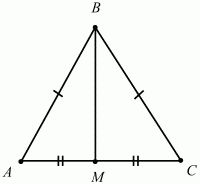
В прямоугольном треугольнике АВМ катет АМ можно выразить через синус угла АВМ. Этот угол известен и равен 60 градусам, а значит, известны и значения синуса и косинуса этого угла. Поскольку АМ – противоположность, а значит, для его нахождения нужно воспользоваться формулой синуса.
$$Sin(ABM)={AM\над AB}$
С другой стороны, синус 60 градусов известен заранее и равен $$\sqrt{3} \over 2$$ . Таким образом, мы можем выразить значение AM:
$$AM=AB*sin(ABM)=AB* {\sqrt{3}\over 2}$
Все стороны треугольника равны между собой, поэтому для простоты обозначим их буквой а.
AB=AC=BC=а
Тогда формула будет выглядеть так:
$$AM=a*{\sqrt{3}\over2}$
Теперь вспомним классическую формулу площади треугольника:
$S= {1\over2}h*a$, где a — основание треугольника, h — высота, проведенная к этому основанию. В данном треугольнике это будет выглядеть так:
$$S={1\over2}*BC*AM={1\over2}*a*a*{\sqrt{3}\over2}=a^2*{\sqrt{3}\over4}$
BC заменили на a, так как все стороны равны между собой, а значение высоты мы нашли ранее. Полученная формула значительно проще классических по количеству требуемых параметров. Чтобы найти площадь правильного треугольника, достаточно знать значение одной из сторон. Это возможно из-за подобия углов такого треугольника.
Только в правильном треугольнике возможно нахождение площади полной поверхности через сторону.
По этой же причине нельзя использовать эту формулу для равнобедренного или произвольного треугольника. Прежде чем использовать эту формулу, необходимо доказать, что треугольник правильный, или убедиться, что это условие задано в исходных данных задачи.
Что мы узнали?
Мы научились находить площади правильного треугольника рядом друг с другом, и выяснили, как легко и быстро вывести эту формулу. Запомнив ход вывода, вы сможете использовать это в дальнейшем, не запоминая точных значений, а просто проверив себя, извлекая формулу в черновик.








Комментирование закрыто