
Перпендикулярные линии образуют целый пласт фигур, построений и расчетов в геометрии. Не понимая перпендикулярных линий, вы не сможете решать такие формы, как прямые углы, прямоугольники, квадраты или прямые трапеции. Поэтому стоит уделить этим понятиям особое внимание.
Что такое перпендикулярные прямые
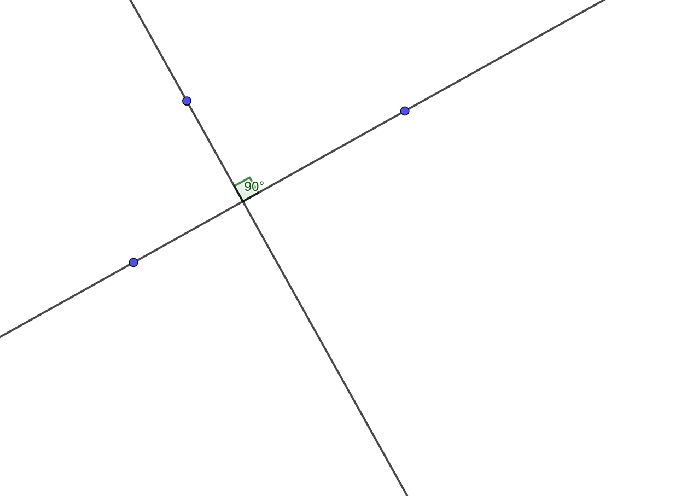
При пересечении двух прямых образуются 4 угла. Определение перпендикулярных линий следующее: это линии с углом 90 градусов. Углов всего 4, полный угол 360 градусов. Если один из углов равен 90 градусов, то остальные 3 будут по 90 градусов.
Чтобы отрезки назывались перпендикулярными, необходимо выполнение следующего условия: отрезки могут пересекать или не пересекать друг друга, но угол пересечения между прямыми, на которых они лежат, должен быть равен 90 градусам.
Свойства
Перпендикулярные линии не обладают многими свойствами. Все они не требуют доказательства, так как основаны на определении перпендикуляра.
- Если каждая из двух прямых перпендикулярна третьей, то эти прямые параллельны. А параллельны они потому, что образующиеся односторонние углы в сумме составят 180 градусов. Это означает, что прямые параллельны по 3-му критерию параллельности. Это свойство можно доказать с помощью любого из трех критериев параллелизма.
- Перпендикулярный отрезок от точки к прямой (или отрезку) будем называть расстоянием от точки до прямой (или отрезка).
- Расстояние от прямой до прямой также является правильным перпендикуляром, опущенным из точки прямой на другую прямую. (под этим понятием подразумеваются параллельные и пересекающиеся прямые).
- Если расстояние между ними не меняется на всем протяжении двух прямых, то прямые будут параллельны.
Фигуры с перпендикулярными прямыми
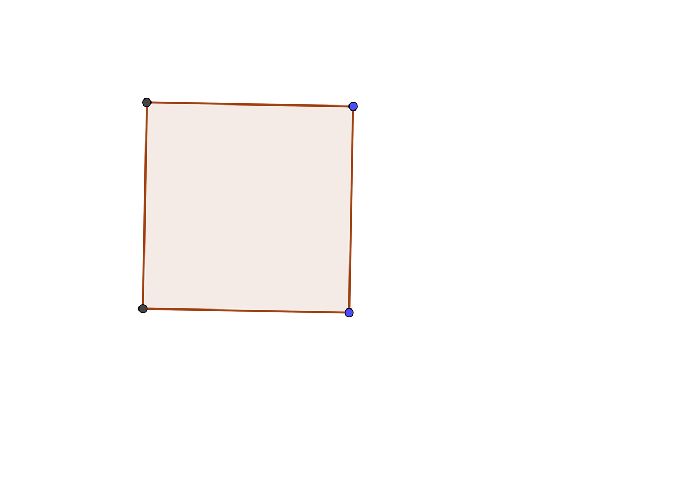
Одними из первых фигур, с которыми знакомится человек, являются квадрат и прямоугольник.
Прямые углы приятны человеческому взгляду, поэтому очень часто квадрат или прямоугольник используют как форму для столешниц, стульев, тумбочек и других предметов. Весь окружающий человека мир составлен из параллельных и перпендикулярных линий.
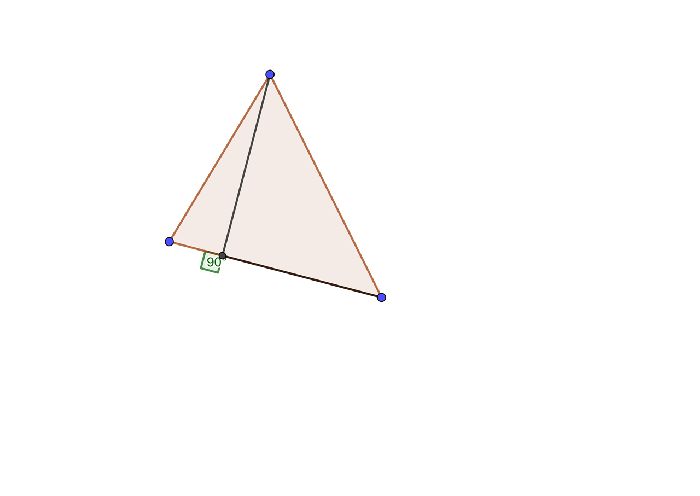
Еще со времен Древней Греции известен прямоугольный треугольник. Форму прямоугольного треугольника принимали различные приборы для навигации, кроме того, много времени изучению свойств прямоугольного треугольника уделил Пифагор. Именно его авторству принадлежит Теорема Пифагора, которая часто востребована в решениях задач.
Это прямоугольная трапеция, у которой одна из сторон перпендикулярна обоим основаниям. А стереометрия и вовсе полна перпендикуляров в пространстве: правильная призма, прямоугольная пирамида и самый обычный куб.
Кроме того, в любом треугольнике можно провести высоту, необходимую для нахождения площади фигуры. Угол угла для нахождения площади пригодится и в параллелограмме, а прямоугольный треугольник и квадрат имеют в составе сторон высоту, благодаря чему найти площадь этих фигур гораздо проще.
Что мы узнали?
Мы рассмотрели, что такое перпендикулярные линии, поговорили о свойствах перпендикуляров и описали формы, для построения которых необходимы перпендикулярные линии. Тему мы поняли для полного понимания, когда впервые столкнулись с этой проблемой в 6 классе.








Комментирование закрыто