
В школьном курсе геометрии изучаются разные виды треугольников. В задачах часто рассматривается остроугольный треугольник, поэтому свойства этой фигуры стоит изучить особенно внимательно.
Определение понятия
Треугольник – это фигура, состоящая из трёх точек и трёх соединяющих их отрезков. В зависимости от углов треугольник может быть:
- Прямоугольный, если один из углов равен 90 градусам;
- Тупой, если один из углов тупой, т.е более 90 градусов;
- Остроугольный, если все углы треугольника острые.
Для решения задач с остроугольными треугольниками часто приходится использовать теорему синуса или косинуса.
Еще в Древней Греции математики изучали треугольники. Именно греки разработали основы современной геометрии, куда входит и множество теорем о треугольниках. Например, автор теоремы Пифагора родом из Древней Греции.
Характеристики
В остроугольном треугольнике каждый угол меньше 90 градусов. Но сумма углов в треугольнике всегда равна 180. На любой фигуре вершины обозначаются заглавными буквами.
Одним из элементов треугольника, наряду со сторонами и углами, является внешний угол. Внешний угол – это угол, примыкающий к внутреннему углу треугольника.
Любой треугольник имеет 6 внешних углов, по 2 на каждый внутренний. Любой внешний угол остроугольного треугольника всегда будет тупым.
Линии остроугольного треугольника
Остроугольный треугольник обладает рядом свойств.
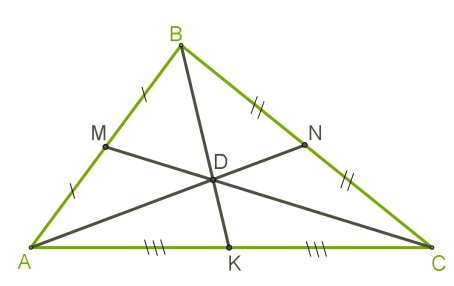
Медиана геометрической фигуры делит пополам сторону, на которой она опущена. Причем этот отрезок можно провести из любой вершины. Медианы пересекаются в одной точке, и эта точка делит каждую из них в соотношении 2:1.
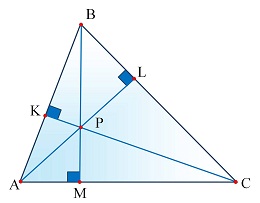
Известно, что если провести в остроугольном треугольнике три высоты, то они пересекутся в одной точке, которая называется ортоцентром. Эти сегменты опущены под прямым углом к противоположным сторонам. Высоты остроугольного треугольника делят эту фигуру на прямоугольные треугольники.
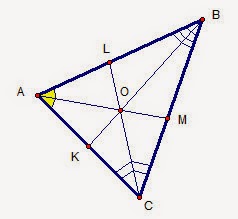
Биссечения в остроугольном треугольнике не просто делят углы пополам. Эти отрезки пересекаются в точке, которая является центром вписанной окружности.
Также биссектриса делит сторону остроугольного треугольника на две части, пропорциональные соответствующим сторонам. Это утверждение необходимо запомнить для решения некоторых задач.
Свойства
Если просуммировать числовые значения двух сторон остроугольного треугольника, то обязательно получим число, которое будет больше третьего отрезка этой геометрической фигуры.
Средняя линия в остроугольном треугольнике параллельна одной из сторон данной фигуры и равна ее половине.
Что мы узнали?
В остроугольном треугольнике каждый угол меньше 90 градусов. Общая сумма углов здесь также равна 180 градусов. Нельзя забывать характерные линии треугольника. Потому что с их помощью легко вычислить стороны заданной треугольной фигуры или центр определенного круга. А если в условиях задач по геометрии заданы углы, то можно использовать тригонометрические функции.








Комментирование закрыто