
Знание знаков подобия треугольников и умение использовать эти знаки открывают новые пути решения задач. Иногда студенты ставятся в тупик, когда необходимо определить соотношение площадей подобных треугольников из-за новизны подхода к выводу формулы. Рассмотрим сам вывод, чтобы понять принцип и использовать его в дальнейшем для решения задач.
Подобие
Подобные треугольники – это треугольники, у которых длины всех сторон пропорциональны друг другу и углы равны. Отношение соответствующих сторон в подобных треугольниках всегда равно одному и тому же числу, которое называется коэффициентом подобия.
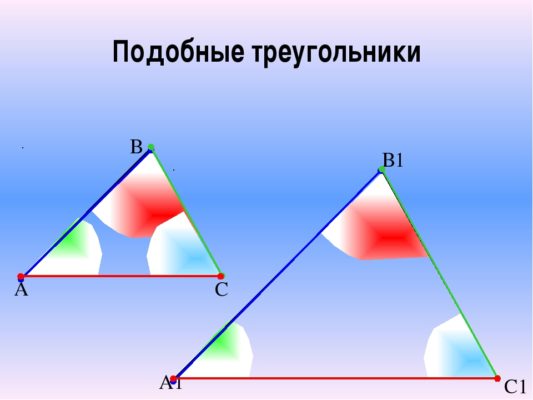
Коэффициент подобия часто используют для решения задач о подобных треугольниках, поскольку можно найти коэффициент через одно отношение, а затем выразить неизвестную сторону через известную. Коэффициент подобия обозначается буквой k.
Не нужно зацикливаться только на треугольниках. Хотя признаки подобия выведены только для них, любая фигура в геометрии имеет подобную. То же касается и равенства фигур: любая фигура в геометрии имеет равную себе, ведь равенство это частный случай подобия с коэффициентом k=1

Признаки подобия
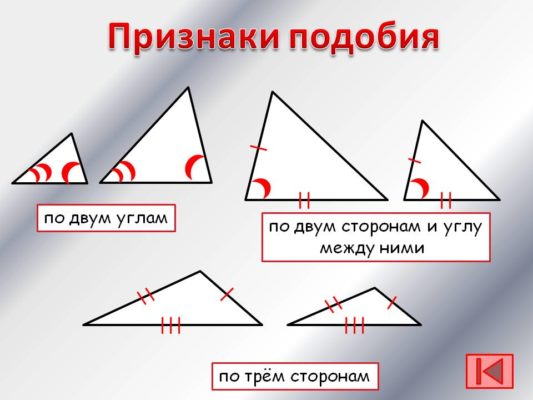
Сегодня для любого треугольника существует 3 критерия подобия.
- На двух углах. Если два угла одного треугольника равны двум углам другого треугольника, то эти треугольники равны.
- По бокам и углу между ними. Если две стороны треугольника пропорциональны двум сторонам другого треугольника, а углы между этими сторонами равны, то такие треугольники подобны.
- На трёх страницах. Если три стороны треугольника пропорциональны трем сторонам другого треугольника, то эти треугольники подобны.
Чтобы доказать пропорциональность сторон, нужно вычислить отношение длин соответствующих сторон. Для пропорциональных сторон результаты будут такими же.
У пропорциональны треугольников будут также пропорциональны и все характеризующие отрезки: высота, медиана, биссектриса. Коэффициент подобия одинаков для всех отрезков треугольника. Этот факт нужно запомнить, он важен для решения многих задач и выведения формулы отношения площадей подобных треугольников.
Площади подобных треугольников
Рассмотрим два подобных треугольника ABC и $A_1B_1C_1$. Площадь треугольника равна половине произведения основания на высоту.
$$S={1\over{2}}t*AB$$, то площадь второго треугольника равна:
$$S_1={1\over{2}}t_1*A_1B_1$
Если разделить одну область с другой, получится следующее соотношение:
$${S\over{S_1}}={{h*AB}\over{h_1*A_1B_1}}$$ если вспомнить, что отношение сторон подобных треугольников равно коэффициенту подобия, то получим следующее результат:
$${S\over{S_1}}=k*k=k^2$$ – то есть площади подобных треугольников относятся друг к другу с коэффициентом пропорциональности, равным коэффициенту подобия в других
Что мы узнали?
Мы вспомнили, что это за цифры. Мы говорили о подобных треугольниках. Выявлены три признака сходства между треугольниками. Мы обнаружили, что коэффициент подобия можно использовать не только для работы со сторонами треугольников, но и для всех характеризующих отрезков. Мы вывели формулу отношения площадей подобных треугольников.








Комментирование закрыто