
Медиана треугольника, как и высота, выступает графическим параметром, определяющим весь треугольник, величину сторон и углов. Три значения: медианы, высоты и биссектрисы — это как штрих-код на товаре, наша задача — просто уметь его посчитать.
Определение
Медиана — это отрезок, соединяющий высоту и середину противоположной стороны. Треугольник имеет три вершины, а значит, и три медианы. Медианы не всегда совпадают с высотами или биссектрисами. Чаще всего это отдельные сегменты.
Свойства медиан
- Медиана равнобедренного треугольника, проведенная к основанию, совпадает с высотой и биссектрисой. В равностороннем треугольнике все медианы совпадают с биссектрисой и высотой.
- Все медианы треугольника пересекаются в одной точке.
- Медиана делит треугольник на два треугольника равной площади, а три медианы делят треугольник на 6 треугольников одинаковой площади.
Равновеликими называют треугольники, площади которых равны.
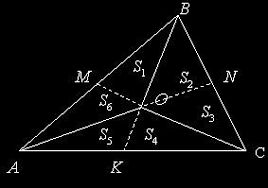
- Пересечение медиан делит их в соотношении 2:1, считая от вершины.
- Медиана, проведенная к гипотенузе прямоугольного треугольника, равна половине гипотенузы.
Задачи
Все эти качества легко запомнить, они легко закрепляются на практике. Чтобы лучше понять тему, давайте решим несколько задач:
- В прямоугольном треугольнике известны катеты, равные a=3 и b=4. Найдите значение медианы m, проведенной к гипотенузе c.
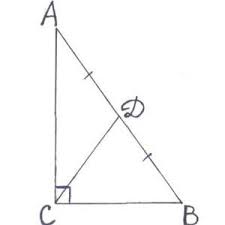
Чтобы найти значение медианы, нам нужно найти гипотенузу, так как медиана, проведенная к гипотенузе, равна половине ее. Гипотенузу находим по теореме Пифагора: $$a^2+b^2=c^2$
$$c=\sqrt{a^2+b^2}=\sqrt{9+16}=\sqrt{25}=5$
Найдем значение медианы: $$m={c\over2}={5\over2}=2,5$$ — полученное число и есть значение медианы.
Значения медиан в треугольнике не равны. Поэтому нужно обязательно представлять, какую именно величину необходимо найти.
- Значения сторон треугольника известны: а=8; б=7; с=9. Найдите значение медианы, опущенной к стороне b.
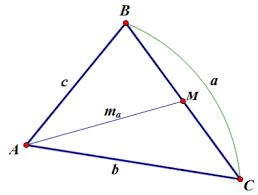
Чтобы решить эту задачу, используйте одну из трех формул для нахождения медианы сторон треугольника:
$$m^2 ={1\over2}*(b^2+c^2-a^2)$
Как видите, здесь главное запомнить коэффициент скобок и знаки по сторонам. Знаки запомнить легче всего — всегда вычитается та сторона, на которую опущена медиана. В нашем случае это одно, но может быть и любое другое.
Подставим значения в формулу и найдем медианное значение: $$m=\sqrt{{1\over2}*(b^2+c^2-a^2)}$
$$m=\sqrt{{1\over2}*(49+81-64)}=\sqrt{33}$$ — оставим результат в беспорядке.
- В равнобедренном треугольнике медиана проведена к основанию 8, а само основание равно 6. Вместе с оставшимися двумя эта медиана делит треугольник на 6 треугольников. Найдите площадь каждого из них.
Медианы делят треугольник на шесть равных частей. Это значит, что площади маленьких треугольников будут равны друг другу. Достаточно найти площадь большего и разделить ее на 6.
Учитывая медиану, проведенную к основанию, в равнобедренном треугольнике это биссектриса и высота. Это означает, что известны основание и высота треугольника. Вы можете найти площадь.
$$S={1\over2}*6*8=24$
Площадь каждого из маленьких треугольников: $${24\over6}=4$
Что мы узнали?
Мы узнали, что такое медиана. Мы определили свойства медианы и нашли решения типичных задач. Мы рассказали об основных ошибках и выяснили, как быстро и легко запомнить формулу нахождения медианы через стороны треугольника.








Комментирование закрыто