
Гипотенус – понятие, пришедшее к нам из Греции, связанное с треугольниками. К каким треугольникам относится это понятие, что оно означает и когда его использовать недопустимо, речь пойдет ниже.
Треугольник
Треугольник – это фигура, состоящая из трёх отрезков (сторон) и трёх точек (вершин). Стороны образуют три угла с тремя вершинами.

Для формулировки теорем требуется всем понятное обозначение сторон. Эти обозначения не обязательно должны быть классическими АВ или ВС, обозначения зависят от каждого конкретного ученика. Никто не вправе запретить решающему обозначать фигуру так, как это удобно лично ему. Например, именно по этой причине в математику было введено понятие основания треугольника. Вспомните, в равнобедренном треугольнике высота, проведенная к основанию, совпадает с биссектрисой и медианой. Формулировка четкая, понятная и простая для запоминания. Именно в этих целях и вводят дополнительные понятия.
Прямоугольный треугольник
Прямоугольный треугольник – особая форма. Он имеет свои свойства и пропорции, один из углов такого треугольника всегда известен и равен 90 градусам, кроме того, существуют конкретные формулы площадей и признаки подобия прямоугольным треугольникам.
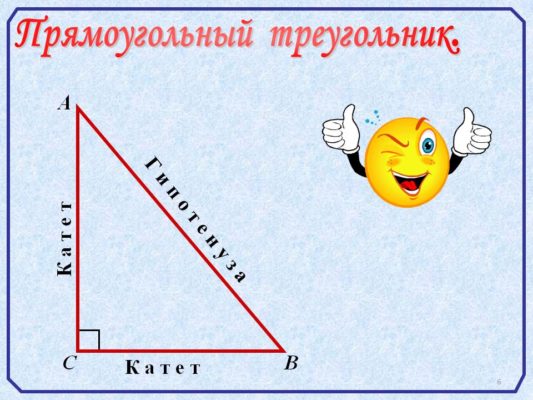
В Древней Греции прямоугольным треугольникам уделяли особое внимание. Эти фигуры были предметом изучения не только математики, но и мореходства. С помощью подобных прямоугольных треугольников греки определяли расстояния в море. А в древних Сиракузах на основе системы прямоугольных треугольников была создана система прицеливания, с помощью которой город долгое время отбивался от атак врагов.
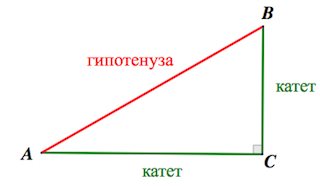
Греки уделяли особое внимание точности формулировок и поэтому придумали особые названия сторонам треугольников: гипотенуза для стороны, противолежащей прямому углу, и катет для сторон, прилежащих к прямому углу.
Есть ли у равнобедренного треугольника гипотенуза? Вообще говоря, нет. Равнобедренный треугольник имеет только две стороны и основание. Но если перед нами прямоугольный равнобедренный треугольник, то основанием такого треугольника будет еще и гипотенуза. Его можно найти как квадратный корень из удвоенного произведения квадрата катета – это следствие теоремы Пифагора и равенства катетов как сторон равнобедренного треугольника.
$b=\sqrt{2a^2}$ – где b – гипотенуза, а a – длина одного из катетов
Равносторонний треугольник
Стоит упомянуть и о равностороннем треугольнике, поскольку это частный случай равнобедренного треугольника. Может ли равносторонний треугольник иметь гипотенузу? Нет, потому что гипотенуза возможна только в прямоугольном треугольнике, а в равностороннем треугольнике все углы всегда равны 60 градусам, поэтому этот вариант вообще невозможен.
Что мы узнали?
Мы узнали, почему требуется большое количество определений. Мы рассказали о том, как достигаются точные формулировки в геометрии, вспомнили древнегреческих учёных и рассказали, для чего они использовали знания о прямоугольных треугольниках. Мы выявили случаи, когда равнобедренный треугольник может иметь гипотенузу, а когда ее существование невозможно. Также мы говорили о возможности существования гипотенузы в равностороннем треугольнике.








Комментирование закрыто