
Средняя линия треугольника является интересным характеризующим отрезком, поскольку она обладает рядом свойств, позволяющих найти простое решение, казалось бы, сложной задачи. Итак, давайте рассмотрим основные свойства средней линии и поговорим о том, как найти длину этого отрезка в треугольнике.
Треугольник и его характеризующие отрезки
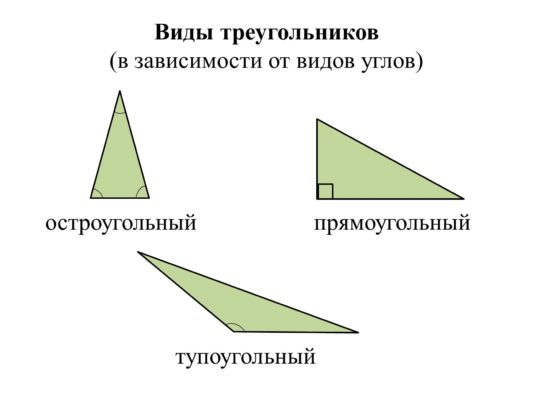
Треугольник – это фигура, состоящая из трёх сторон и трёх углов. В зависимости от величины углов треугольники делятся на:
- Острый угол
- Тупой
- Прямоугольный
Наиболее важными характеристическими сегментами треугольника являются:
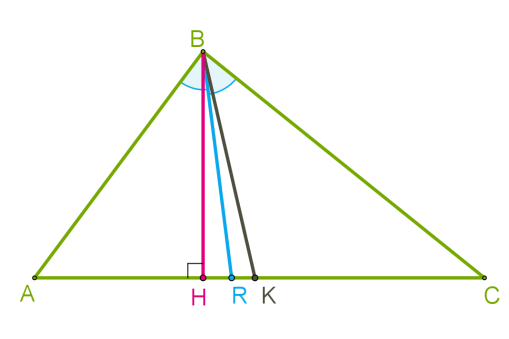
- Медиана — это отрезок, соединяющий вершину с центром противоположной стороны.
- Биссектриса – отрезок, проведенный из вершины угла к противоположной стороне и делящий угол пополам
- Высота — это перпендикуляр, спускающийся из вершины треугольника к прямой, содержащей противоположную сторону.
Для каждого из характеризующих отрезков существует отдельная точка пересечения. Когда вы соединяете три точки пересечения медиан, биссектрис и высот, достигается золотое сечение треугольника.
Однако существует ряд дополнительных характеризующих сегментов:
- Биссектриса — это перпендикуляр, восстановленный из центра стороны. Как правило, биссектрису продолжают до пересечения с другой стороной.
- Средняя линия – это отрезок, соединяющий середины соседних сторон.
- Радиус вписанной окружности. Вписанная окружность – это окружность, касающаяся каждой стороны треугольника. Центр круга — это пересечение биссектрис треугольника
- Радиус описанной окружности. Описанная окружность – это окружность, содержащая все вершины треугольника. Центр описанной окружности является пересечением серединных перпендикуляров треугольника.
Смежными сторонами треугольников называют стороны, которые имеют общую вершину. В геометрии существует понятие противоположных сторон, т.е сторон, которые лежат друг напротив друга и не имеют общих вершин. Но это понятие для треугольников не применимо – любая пара сторон в треугольнике является смежной.
Свойства средней линии
Характеристик средней линии не так много, но все они важны при решении задач. Дело в том, что задач по нахождению длины центральной линии немного, а потому некоторые из них способны обмануть ученика, несмотря на свою простоту.
Поэтому приведем и обсудим все свойства средней линии треугольника:
- Средняя линия треугольника равна половине площади основания. Вообще правильнее говорить не половину основания, а половину противоположной стороны. Так как в треугольнике 3 стороны, но только одно основание. Но в общем случае основанием можно считать любую из сторон треугольника, поэтому такая формулировка считается приемлемой. Более того, этому легче учиться. Обычно это свойство используется для определения длины средней линии треугольника.
- Центральная линия параллельна основанию. Ситуация с понятием фундамента такая же, как и в предыдущем объекте.
- Центральная линия отсекает от треугольника небольшой подобный треугольник с коэффициентом подобия, равным 0,5
- Три средние линии делят треугольник на 4 равных треугольника, равных большому треугольнику с коэффициентом подобия 0,5
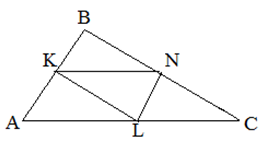
Фактически формула длины центральной линии следует из второго свойства:
$m=1\over{2}*a$- где m — средняя линия, а сторона противоположна средней линии.
Что мы узнали?
Мы говорили о второстепенных характеризующих сегментах, подчеркивающих среднюю линию. Мы дали свойства средних линий и рассказали об особенностях формулировки этих свойств. Они объяснили, как выводится формула длины средней линии треугольника и как средняя линия делит треугольник. Все эти свойства используются при решении треугольников.








Комментирование закрыто