Длина медианы правильного треугольника

Медиана является одним из характеризующих отрезков треугольника, наряду с биссектрисой и высотой. Студентам часто бывает особенно трудно найти медиану. В обычном случае нужно воспользоваться формулой, но для равностороннего треугольника можно вывести упрощенный вариант нахождения медианы.

Необходимые данные

Для вывода формул нужно вспомнить несколько теоретических расчетов:

• Медиана — это отрезок, соединяющий вершину треугольника с серединой противоположной стороны. Три медианы треугольника пересекаются в одной точке.
• В равнобедренном треугольнике медиана проведена к основанию, биссектрисе и высоте. Правильный треугольник — это частный случай равнобедренного треугольника, основанием которого может быть любая из сторон. Это означает, что каждая медиана равностороннего треугольника будет совпадать с соответствующей биссектрисой и высотой.
• В правильном треугольнике все стороны равны, а каждый угол равен 60 градусам.

Нахождение медианы по общей формуле

Для начала воспользуемся общей формулой. Вспомним формулу длины медианы через длины сторон треугольника:

$$m_c={{\sqrt{2a^2+2b^2-c^2}}\over{2}}$

Но в правильном треугольнике все стороны равны между собой:

а=б=с

Заменим в формуле условия равенства и представим аналогичные слагаемые:

$$m_c={{\sqrt{2a^2+2a^2-a^2}}\over{2}}$

$$m_c={{\sqrt{3a^2}}\over{2}}$

Значение ${a^2}$ можно переместить за пределы корня. Затем:

$$m_c={{\sqrt{3a^2}}\over{2}}$

$$m_c={{\sqrt{3}}\over{2}*а}$

Найдите медиану, используя теорему Пифагора

Теперь попробуем вывести ту же формулу, используя теорему Пифагора.

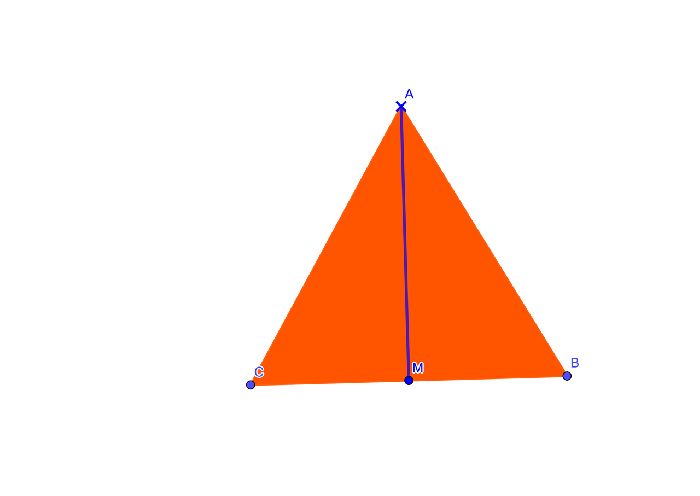
В существующем правильном треугольнике ABC проводим медиану AM. Она будет совпадать с биссектрисой и высотой. Тогда, используя теорему Пифагора, из треугольника АВМ найдем сторону АМ, которая и будет медианой большого треугольника.

$$AM=\sqrt{AB^2-BM^2}$

Но все стороны треугольника равны, а точка М является серединой стороны ВС. Средства:

$$AB=а$

$$VM={1\over2}BC={1\over2}a$

Подставим эти значения в исходную формулу:

$$AM={\sqrt{AB^2-BM^2}}= {\sqrt{a^2-{{a}\over{2}}^2}}= \sqrt{a^2-{{ а^2}\over{4}}}=\sqrt{{3a^2}\over{4}}$

Вынесем значения $a^2$ и 4 за знак корня.

$$AM=\sqrt{{3a^2}\over{4}}=a*{{3}\over{\sqrt{2}}}$

Результатом является та же формула для длины медианы правильного треугольника. Это означает, что вывод первого метода был проведен правильно, и вы можете воспользоваться любым из двух способов, если вдруг забыли формулу нахождения медианы равностороннего треугольника.