
В 10 классе геометрии есть разделы, изучающие свойства диагонали прямоугольного параллелепипеда. Черты изучаются не просто так; много задач на нахождение диагонали этой фигуры встречается на ЕГЭ. Поэтому имеет смысл подробно поговорить о свойствах диагонали прямоугольного параллелепипеда.
Определение понятия
В общем случае диагональ — это отрезок, соединяющий вершины двух углов, не принадлежащих одной стороне многогранника. Прямоугольный параллелепипед, напротив, состоит из шести граней, которые являются прямоугольниками.
Диагонали в прямоугольном параллелепипеде можно проводить не только во внутреннем пространстве фигуры, но и на боковых поверхностях и на поверхностях основания. В последнем случае обычно уточняют, что речь идет о диагонали боковой грани или диагонали основания.
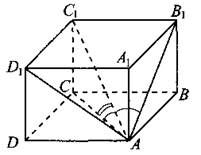
У параллелепипеда есть четыре диагонали. Причем, эти отрезки не принадлежат ни одной боковой грани или основаниям, а проводятся внутри фигуры.
Характеристики диагонали
Существуют две теоремы о диагоналях параллелограмма. Для их доказательства используются дополнительные конструкции. Например, диагональ нижнего основания данной объемной геометрической фигуры часто служит стороной для нескольких треугольников.
Первая Теорема
Квадрат диагонали кубоида можно найти, суммируя квадраты трех измерений этой геометрической фигуры.
Здесь речь идет о длине, ширине и высоте рассматриваемого многогранника. Для доказательства этой теоремы необходимо использовать свойства прямоугольных треугольников.
Диагональ, проведенная в основании, будет гипотенузой прямоугольного треугольника $ABC$, а значит, ее можно найти по теореме Пифагора через сумму квадратов $AB$ и $BC$. А $AB$ и $BC$ — это длина и ширина параллелепипеда.
$$AC=\sqrt{AB^2+BC^2}$
Далее рассмотрим прямоугольный треугольник $ACC’$. Диагональ $AC’$ также можно найти с помощью теоремы Пифагора, как корень суммы катетов $AC$ и $CC’$. Но мы уже нашли $AC$ как корень суммы квадратов $AB$ и $AC$:
$(ACʹ)^2= (CCʹ)^2+(CD)^2+(CB)^2$, где
$CCʹ$ – высота;
$CD$ – длина;
$CB$ – ширина.
Вот как выглядит формула, отражающая содержание этой теоремы.
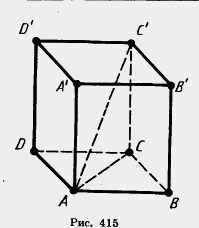
Обычно его длиной считают больший отрезок, расположенный в основании параллелепипеда. Меньший сегмент — это ширина.
Вторая теорема
В любом параллелепипеде четыре диагонали пересекаются в одной точке, называемой точкой симметрии, и делятся ею. Это свойство доказывается рассмотрением двух диагоналей и проведением соответствующих отрезков.
Чтобы доказать эту теорему, мы должны помнить, что плоскость можно определить двумя пересекающимися прямыми. В данном случае сечение плоскости, определяемое двумя пересекающимися диагоналями, имеет форму прямоугольника. А диагонали прямоугольника, как известно, делятся пополам точкой пересечения.
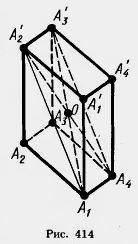
Из этой же теоремы можно сделать вывод о том, что все его диагонали будут равными между собой отрезками.
Что мы узнали?
Мы говорили о диагоналях кубоида. Мы узнали, что, используя свойства диагоналей параллелепипеда, можно найти ширину, длину и высоту параллелепипеда. Мы говорили о том, как найти центр симметрии и определить длину диагоналей прямоугольного параллелепипеда.








Комментирование закрыто