Центральный угол

Круг труден для изучения. Понятие элементов в круге особенно сложно для учащихся. Об одном из таких элементов – центральном угле – и пойдет речь сегодня.

Окружность и круг

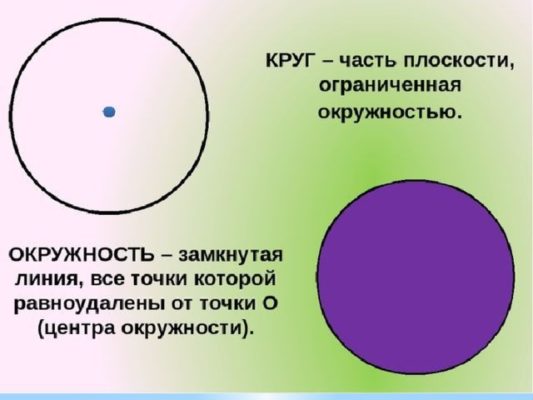
Чтобы обсудить центральный угол, вам нужно понять, что такое круг. Окружность – это совокупность точек, равноудалённых от центра окружности. Круг – это фигура, заключенная в круг, или фигура, ограниченная кругом.

Различие окружности и круга в том, что окружность это линия, а круг – фигура. Поэтому у окружности есть длина, но нет площади. А у круга есть площадь, но нет длины.

Круг и окружность часто путают, а это недопустимо для правильного решения задач.

Центральный угол

Рис. 1. Круг и круг.

Элементы окружности

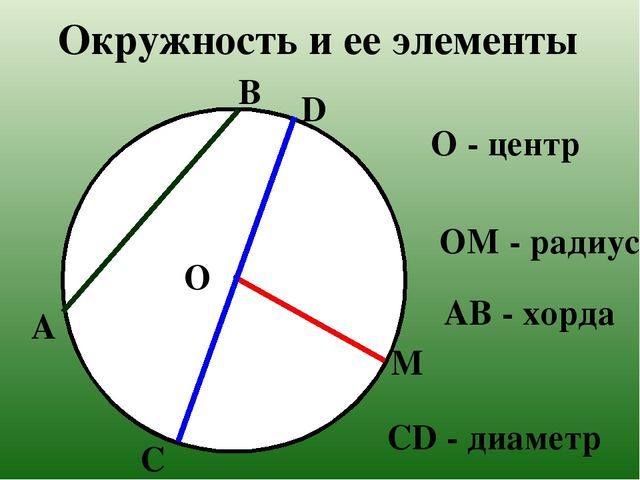
Перечислим основные элементы круга:

  • Хорда – это отрезок, соединяющий две точки окружности.
  • Диаметр – это отрезок, соединяющий две противоположные точки окружности. Диаметр всегда проходит через центр круга и его длина равна длине двух радиусов. Любой диаметр является хордой, но не всякую хорду можно считать диаметром.
  • Радиус – это отрезок, соединяющий точку окружности и центр окружности.
  • Дуга — часть круга, ограниченная углом или сектором
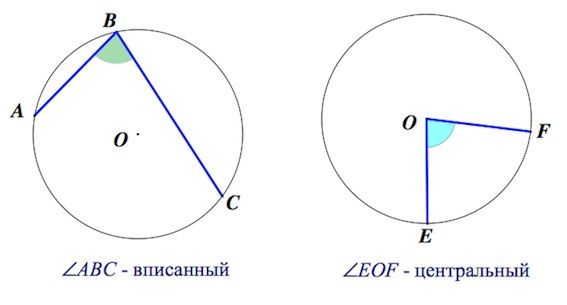
  • Вписанный угол – это угол, вершина которого лежит на окружности.
  • Центральный угол – это угол, вершина которого находится в центре окружности.

Теперь давайте более подробно рассмотрим центральный угол.

Центральный угол

Рис. 2. Элементы по кругу.

Центральный угол и сектор

В общем, дуга используется для измерения всех углов в окружности. Дуга сама по себе является результатом поворота радиуса вокруг центра круга, и поскольку угол также является мерой вращения чего-либо, дуга используется как мера угла и измеряется в градусах.

Теорема о центральном угле гласит, что размер центрального угла равен градусной мере дуги, которую он охватывает. В этом случае величина вписанного угла равна половине градусной меры дуги, на которую он опирается.

Сектором зовется площадь центрального угла. Это часть площади всего круга, поэтому зная формулу площади с помощью центрального угла можно узнать площадь сектора.

Центральный угол

Рис. 3. Вписанные и центральные углы окружности.

Выведем формулу площади сектора. Для этого помните, что полный круг равен 360 градусам. Дуга всей окружности равна одной и той же величине. А центральный угол является частью дуги. Площадь круга равна:

$$S=pi*r^2$

Площадь сектора составляет:

$$S={a\over{360}}*pi*r^2$$ – где a — градусная мера угла части круга.

Таким образом, зная дугу центрального угла, можно найти площадь сектора.

Не забывайте, что любой формулой можно пользоваться как справа налево, так и слева направо. С помощью приведенной формулы можно найти значение центрального угла.

Что мы узнали?

Мы говорили о круге и окружности. Узнайте, чем они отличаются. Выявлены основные элементы круга и круга. Дано определение центрального угла. Нам рассказали, как найти центральный угол через дугу окружности и сектор. Мы вывели формулу площади сектора круга.