
Боковая сторона равнобедренного треугольника – довольно интересное явление, поскольку ее часто просят найти в простых геометрических задачах. Самое главное в поиске страницы — знание основного метода решения, да и сам процесс не представляет сложности.
Равнобедренный треугольник
Равнобедренный треугольник – это треугольник, у которого две стороны равны, а третья – основание.
Только в равнобедренном треугольнике основание имеет реальное практическое применение. Для лучшего визуального восприятия фигуры стоит располагать чертеж так, чтобы основание располагалось снизу. При этом равносторонний треугольник считается частным случаем равнобедренного. В равностороннем треугольнике любая сторона может считаться как основанием, так и боковой. При этом равносторонний треугольник можно построить, зная только одну сторону. Построение равнобедренного треугольника по боковой стороне невозможно, нужно знать значение основания или угол между сторонами.
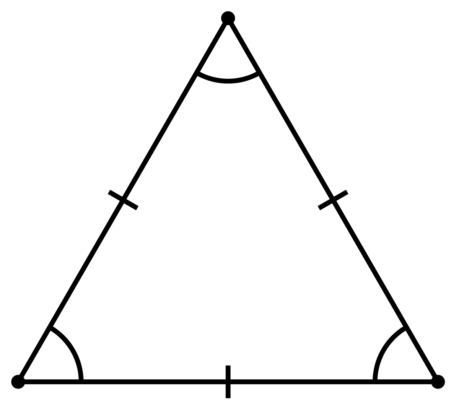
Свойства равнобедренного треугольника
Свойства равнобедренного треугольника не так уж и велики. Для решения школьных задач даже в старших классах используются всего 3 свойства:
- Стороны треугольника равны.
- Биссектриса треугольника совпадает с медианой и высотой.
- Углы при основании равнобедренного треугольника равны.
Этих свойств вполне достаточно, чтобы использовать стиль решения, неприменимый ни к одному другому треугольнику.
Боковая сторона треугольника
Равнобедренные фигуры отличаются от остальных тем, что для решения всего треугольника достаточно двух показателей, из которых хотя бы один должен быть стороной.
Если знать основание и некоторые углы, найти сторону несложно. Если опустить высоту до основания, совпадающего с медианой и биссектрисой, то получится два маленьких равносторонних треугольника, стороной которых будет гипотенуза.
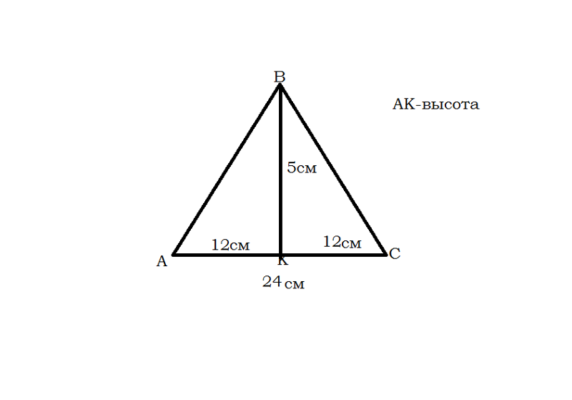
Сторону можно найти из тригонометрической функции синуса или косинуса. Выбор функции зависит от того, какой угол известен. Для этого вам понадобится одна из ножек. Одна из ножек — высота и не всегда ее можно найти. Чаще всего используется ножка, соответствующая половине основания. Почему оно равно половине основания? Потому что основание делится пополам нарисованной высотой, так как совпадает с медианой.
Другая сторона аналогична найденной. Кстати, такой стиль решения используется практически во всех задачах о равнобедренном треугольнике, так что об этом стоит помнить.
Тригонометрическую функцию известного угла можно определить по таблицам Брадиса. В этих таблицах рассчитаны значения для всех существующих целых и промежуточных углов.
Равнобедренный треугольник не может быть решен, если:
- известны только 2 стороны;
- известны только углы;
- известен только фундамент;
- известно лишь значение некоторых характеризующих отрезков: высоты, медианы, биссектрисы и т д.
Во всех остальных случаях треугольник можно решить, даже если известны только площадь и один из углов. Зачем знать варианты, когда решение заведомо невозможно? Чтобы не попасть в ловушку неразрешимых проблем. Это редкость, но они случаются. Предлагая их к решению, составители проверяют уровень знаний учащихся о рисунке.
Что мы узнали?
Мы рассказали о том, что такое равнобедренный треугольник, выделили его основные свойства и рассказали о методах нахождения сторон равнобедренного треугольника. Также мы выделили отдельно сторону и рассказали, как можно легко и быстро определить значение стороны равнобедренного треугольника.








Комментирование закрыто