
Полупроводник равнобедренного треугольника обладает особым свойством, определяющим стиль решения задач по нахождению элементов равнобедренного треугольника. Чтобы лучше понять важность решения подобных задач, поговорим о биссектрисе равнобедренного треугольника.
Определения
Равнобедренный треугольник – это треугольник, две стороны которого равны друг другу. Третья сторона называется основанием, углы при основании равны.
Биссектриса треугольника – это отрезок, который делит угол треугольника на две равные части. Каждая точка биссектрисы равноудалена от каждой из сторон треугольника, т.е если из любой точки биссектрисы опустить перпендикуляры к каждой стороне угла, то эти перпендикуляры будут равны между собой. Точка пересечения биссектрис является центром вписанной окружности треугольника и называется инцентром треугольника.

Биссектриса равнобедренного треугольника
Равнобедренный треугольник уникален, поскольку его две стороны и два угла равны. Именно этим обеспечивается главное свойство биссектрисы равнобедренного треугольника: в равнобедренном треугольнике биссектриса, проведенная к основанию, совпадает с высотой и медианой.
В равнобедренном треугольнике только биссектриса, проведенная к основанию, совпадает с высотой и медианой. Две другие биссектрисы будут отличатся от соответствующих медиан и высот, проведенным к этим же сторонам. Это стоит запомнить раз и навсегда, чтобы не допускать нелепых ошибок.
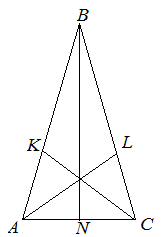
Решая задачи, помните, что это свойство можно использовать не только в равнобедренном, но и в равностороннем треугольнике.
Ведь если выбрать любую из сторон равностороннего треугольника и взять ее за основу, то две другие стороны будут равны, и поэтому равносторонний треугольник можно считать равносторонним треугольником, где основанием может выступать любая сторона.
А поскольку за основание можно принять любую сторону, то каждая биссектриса будет совпадать с соответствующей медианой и высотой. Ведь каждая биссектриса будет притянута к стороне, которую можно считать основанием.
Именно на этом свойстве основано подобие двух треугольников, которое получается в равнобедренном треугольнике в результате проведения биссектрисы. В таких треугольниках одна сторона, одна и та же биссектриса, будет общей.

Биссектриса совпадает с высотой, а это значит, что два маленьких треугольника будут прямоугольными, а биссектриса дает два равных угла. То есть два треугольника будут равны по стороне и прилежащему к ним острому углу, который соответствует одному из знаков равенства прямоугольных треугольников.
На практике часто встречается использование двух маленьких треугольников. Например, если известны основание треугольника и сторона и нужно найти биссектрису, сделать это можно гораздо проще, чем в других треугольниках.
Биссектриса совпадает с медианой и высотой и, следовательно, станет катетом небольшого прямоугольного треугольника, поэтому значение биссектрисы можно найти как значение катета с помощью теоремы Пифагора.
Что мы узнали?
Мы вспомнили, что такое равнобедренный треугольник. Мы рассказали о свойствах биссектрисы равнобедренного треугольника и отдельно выделили свойства биссектрисы равностороннего треугольника. Мы отметили наиболее часто используемый и простой способ нахождения биссектрисы равнобедренного треугольника.








Комментирование закрыто