
Аксиома параллельных прямых – один из постулатов евклидовой геометрии, на котором строится доказательство всех современных теорем стереометрии. Это определение не только математическое, но и историческое. Именно о формулировках, истории появления и интересных особенностях, вытекающих из этих высказываний, и пойдет сегодня речь.
Немного истории
Почти все современные источники приписывают формулировку аксиомы Евклиду, но на самом деле основоположник геометрии сформулировал несколько иную аксиому, точнее даже не аксиому, а скорее знак. Интересно, что это долго пытались опровергнуть, но сегодня остановились.
Пятый постулат или аксиома Евклида звучит так: Если при пересечении двух прямых третьей, сумма односторонних углов менее 180 градусов, то такие прямые пересекаются, при том с той стороны, где сумма углов меньше 180.
Вам ничего не напоминает? Конечно, это третий признак параллельных линий, вывернутых наизнанку: параллельны две прямые, у которых сумма односторонних углов составляет 180 градусов.
А современная интерпретация аксиомы: Через точку на плоскости можно провести одну и только одну прямую, параллельную данной, — принадлежит другому древнегреческому математику — Проклу. Вот небольшая историческая ошибка.
Формулировка
Но кем бы ни был автор аксиомы, в любой задаче и в любом доказательстве надо помнить: утверждение называется аксиомой параллельных прямых и формулируется так: через точку на плоскости можно провести только одну прямую, параллельную данный.
Следствия
Эта аксиома имеет два следствия, которые еще называют свойствами параллельных прямых.
На самом деле, следствий три, но третье в своем доказательстве имеет не только аксиому, а поэтому следствием в полной мере считаться не может. Формулируется третье следствие так: Если прямая перпендикулярна одной из двух параллельных прямых, то она перпендикулярна и второй. Мы докажем это утверждение чуть позже.
Первое следствие аксиомы параллельных прямых звучит так: если прямая параллельна одной из параллельных прямых, то она параллельна третьей.
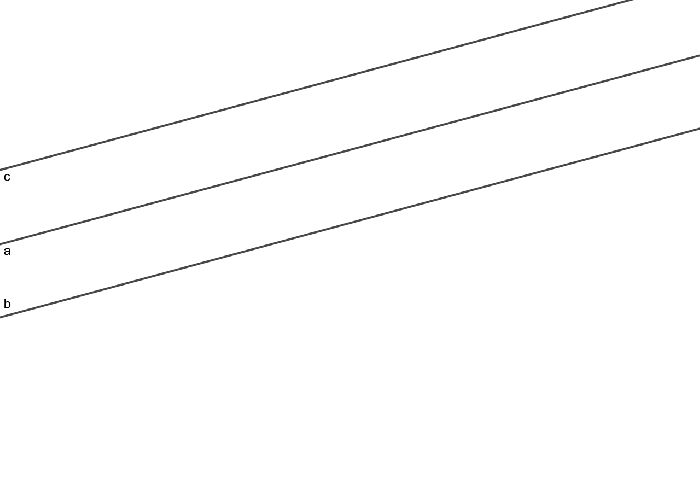
Второе следствие: если линия пересекает одну из параллельных прямых, она также пересечет и другую.
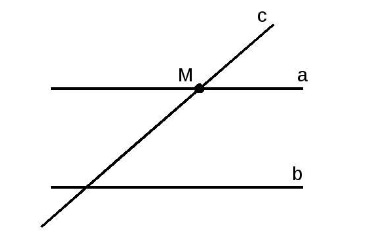
Оба следствия могут быть доказаны от противного.
Задача
Студенты всегда доказывают, что третье последствие является проблемой. Значит необходимо доказать, что если прямая перпендикулярна одной из двух параллельных прямых, то она перпендикулярна и другой.
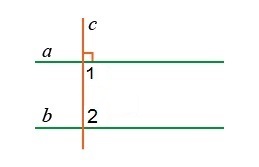
Проведем две параллельные прямые а и б.Линия с перпендикулярна прямой а.Это означает, что линия с пересекает линию а, то есть по следствию 2 из аксиомы параллельных прямых линия с будет также пересекать линию b, так как b и a параллельны.
Рассмотрим углы 1 и 2 — они односторонние с параллельными прямыми а и б и поперечные с. Это означает, что сумма этих углов по свойству параллельных прямых должна быть равна 180 градусам. Но угол 1 известен, так как а перпендикулярен с, то угол равен 90 по определению перпендикуляра.
Найдем угол 2.
$$<1+<2=180$
$$<1=90$
$$<2=180-<1$
$$<2=180-90=90$
Это означает, что линия c перпендикулярна линии b по определению перпендикуляра.
Это следствие можно использовать так же, как и другие, но нет причин забывать, что оно не является следствием в полном смысле слова.
Что мы узнали?
Мы рассказали об истории формулировки аксиомы параллельных прямых, узнали автора аксиомы и привели из нее три результата, доказавших третий.








Комментирование закрыто