
В геометрии часто рассматривают углы треугольника, поскольку этими параметрами удобно пользоваться при различных вычислениях с помощью тригонометрических функций и в доказательствах.
Определение
Углы треугольника формируются с помощью его пересекающихся сторон. Иными словами, два отрезка, выходящие из одной точки образуют геометрическую фигуру, обозначающую часть плоскости, которая и называется углом.
По количеству углов формируются названия многоугольников. Треугольник так называется, потому что содержит 3 угла.
Виды углов треугольника
Используя значения углов произвольных треугольников можно выделить ряд важных свойств геометрических фигур. Так, из евклидовой геометрии известно, что сумма углов произвольного треугольника равняется 180 градусов.
Треугольники классифицируют в зависимости от величины углов. Если один из углов данной геометрической фигуры равняется 90 градусов, то треугольник называют прямоугольным.
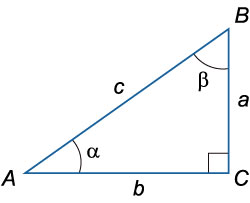
Здесь сторону AB именуют гипотенузой, а отрезки $BC$ и $AC$ будут катетами. Углы $α$ и $β$ всегда острые.
С помощью прямоугольного треугольника выводят тригонометрические тождества. А теорему Пифагора можно выразить формулой $с^2=a^2+b^2$, где квадрат гипотенузы равен сложению квадратов катетов.
Когда один из углов треугольника больше, чем 90 градусов, этот треугольник называется тупоугольным.
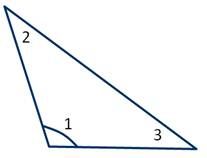
Из теоремы о неравенстве треугольника известно, что когда в этой геометрической фигуре один из углов является прямым или тупым, то сумма двух других углов составит не более 90 градусов, т. е. два других угла обязательно должны быть острыми.
Любой произвольный треугольник можно разделить на два прямоугольных треугольника, если опустить высоту из вершины этой фигуры на противоположную сторону. А тупоугольный треугольник одной из высот наоборот достраивается до большого прямоугольного треугольника.
Значение
Нахождение неизвестных углов и сторон рассматриваемого треугольника, с использованием известных значений, называется «решением треугольников».
Для этого обращаются к общим тригонометрическим теоремам, а также признакам равенства и подобия треугольников.
Что мы узнали?
В произвольном треугольнике углы определяют вид фигуры и возможность существования такой фигуры вовсе. Иногда в задаче достаточно доказать, что такая фигура существовать не может. Знание вида треугольника, позволяет использовать свойства этого треугольника и различные дополнительные построения.








Комментирование закрыто