
Биссектриса – одно из основных понятий в курсе геометрии. Особая роль отводится понятию биссектрисы угла треугольника. В статье мы познакомимся с понятием биссектрисы, с ее свойствами, а затем решим задачу на закрепление материала.
Определения понятия биссектрисы
Биссектриса треугольника – это отрезок, который делит угол треугольника на два равных угла. Например, если угол треугольника равен 1200, проведя биссектрису, мы построим два угла по 600.
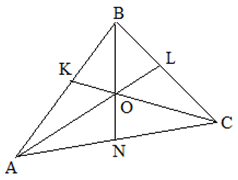
А поскольку в треугольнике три угла, то можно провести три биссектрисы. У них у всех одна точка отсечки. Эта точка является центром окружности, вписанной в треугольник. По-другому эту точку пересечения называют центром треугольника.
При пересечении двух биссектрис внутреннего и внешнего угла получается угол 900. Внешний угол треугольника — это угол, примыкающий к внутреннему углу треугольника.
Биссектриса делит противоположную сторону на два отрезка, которые соединяются сторонами:
$${CL\over{LB}} = {AC\over{AB}}$
Точки биссектрисы равноудаленные от сторон угла, это значит, что они находятся на одинаковом расстоянии от сторон угла. То есть, если из любой точки биссектрисы опустить перпендикуляры на каждую из сторон угла треугольника, то эти перпендикуляры будут равны..
Если вы проведете медиану, биссектрису и высоту из одной вершины, медиана будет самым длинным отрезком, а высота — самым коротким.
Некоторые свойства биссектрисы
В некоторых видах треугольников биссектриса обладает особыми свойствами. В первую очередь это относится к равнобедренному треугольнику. У этой фигуры две одинаковые стороны, а третья называется основанием.
Если провести биссектрису из вершины угла равнобедренного треугольника к основанию, она будет обладать свойствами и высоты, и медианы. Следовательно, длина биссектрисы совпадает с длиной медианы и высотой.
Определения:
- Высота – это перпендикуляр, идущий вниз из вершины треугольника к противоположной стороне..
- Медиана – это отрезок, соединяющий вершину треугольника и середину противоположной стороны.
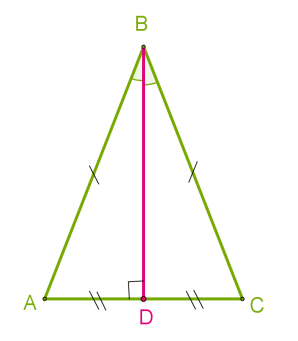
Это также относится к равностороннему треугольнику, то есть треугольнику, у которого все три стороны равны.
Пример задания
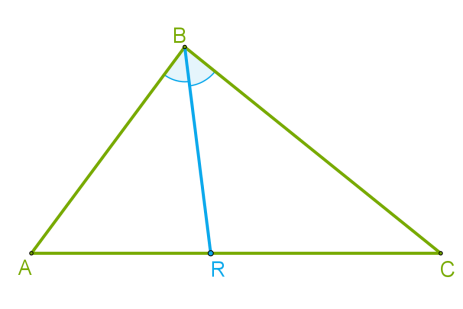
В треугольнике ABC: BR — биссектриса, при этом AB = 6 см, BC = 4 см и RC = 2 см. Вычтите длину третьей стороны.
Решение:
Биссектриса делит сторону треугольника в определенной пропорции. Давайте воспользуемся этой пропорцией и выразим AR. Тогда найдем длину третьей стороны как сумму отрезков, на которые эта сторона была разделена биссектрисой.
- ${AB\over{BC}} = {AR\over{RC}}$
- $RC={6\over{4}}*2=3 см$
Тогда весь отрезок равен AC = RC+ AR
АС = 3+2=5 см.
В равнобедренном треугольнике биссектриса, проведенная к основанию, делит треугольник на два равных прямоугольных треугольника.
Что мы узнали?
Изучив тему биссектрисы, мы узнали, что она делит угол на два равных угла. А если нарисовать его равнобедренным или равносторонним треугольником до основания, то он будет обладать свойствами и медианы, и высоты одновременно.








Комментирование закрыто