
Понятие масштаба знакомо каждому, кто видел географические карты. В географии и топографии используются различные типы масштабов. Рассмотрим понятие числового масштаба более подробно.
Определение численного масштаба
Числовой масштаб выражается в виде дроби, где числитель равен единице, а знаменатель — число, показывающее, во сколько раз изображение было уменьшено.

в России приняты следующие стандартные виды численного масштаба: $${1 : 1000000}, {1 : 500000}, {1 : 300000}, {1 : 200000}, {1 : 100000},$$ $${1 : 50000}, {1 : 25000}, {1 : 10000} $.
Пример
На каком расстоянии будет находиться изображение объекта высотой 600 м, если числовой масштаб ${1 : 50000} ?$
Знаменатель числовой шкалы указывает на то, что длина здания на изображении будет в 50 000 раз меньше его фактической длины.
Фактическая длина объекта составляет 600 м.
Следовательно, длина объекта на изображении составит $${600\более 50000} = 0,012 м = 1,2 см. $
Теперь рассмотрим обратную задачу.
Пример
Изображение объекта на карте имеет длину 1,5 см. Числовой масштаб ${1 : 10000}$. Какова реальная длина объекта?
Длина изображения будет в 10 000 раз меньше фактической длины. Другими словами, фактическая длина будет в 10 000 раз больше длины изображения.
Длина изображения 1,5 см, или 0,015 м.
Следовательно, фактическая длина объекта равна $${0,015*10000} = 150 м. $
Зная размеры исходного объекта и изображения, вы сможете определить числовой масштаб.
Пример
Фактическая длина объекта 500 м, а длина изображения на карте 1 см. Найдите численный масштаб изображения.
Выразим длину изображения в метрах: 1 см = 0,01 м.
Определим соотношение сторон: ${500\более 0,01} = 50000.$
Следовательно, числовой масштаб равен ${1 : 50000}.$
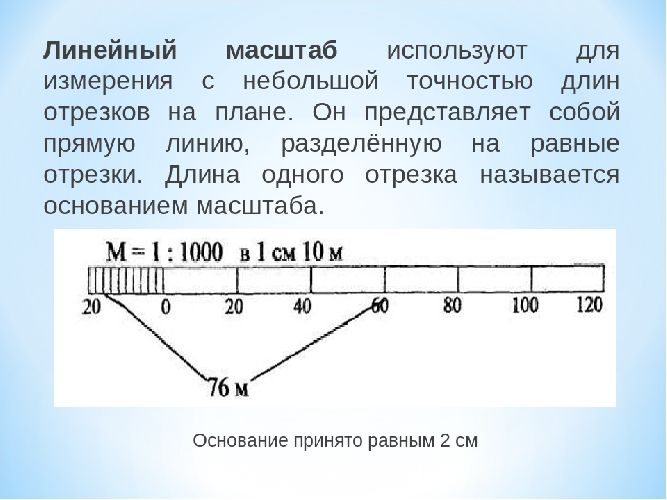
Кроме численного, есть еще другие виды масштаба (рис. 2), например, линейный масштаб, который представляет собой график, построенный в виде разделенного на равные части отрезка прямой.
Линейный масштаб позволяет строить и измерять расстояния на картах без вычислений (рис. 2).
Точность масштаба
Предполагается, что размер сегмента карты, который можно измерить или нанести, составляет 0,01 см.
На основе этого значения вводится понятие точности масштабирования.
Число метров, соответствующее длине 0,01 см в масштабе данной карты, называется максимальной графической точностью этого масштаба.
Из определения точности шкалы следует, что для ее определения нужно знаменатель числовой шкалы разделить на 10 000.
Пример
Масштаб карты ${1\более 2500}$. Знаменатель шкалы равен 2500.
Следовательно, точность масштабирования этой карты составляет ${2500\более 10000} = 0,25 м$.
Что мы узнали?
Мы узнали определение числового масштаба и научились использовать это понятие для решения проблем. Мы узнали, что на практике используются другие виды шкал, например линейные. Мы также узнали определение точности масштабирования и научились ее рассчитывать.








Комментирование закрыто