
Равнобедренный треугольник имеет ряд свойств, которые отличают его от произвольной фигуры. Именно эти свойства во многом помогают решению задач, связанных с равнобедренным треугольником. В этой статье мы подробно разберем каждый из признаков, приведем доказательства и поговорим об обратных теоремах.
Теорема 1
В равнобедренном треугольнике углы при основании равны.
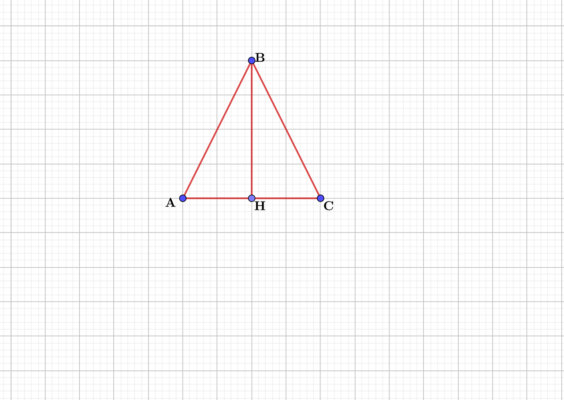
Это свойство углов равнобедренного треугольника можно легко и быстро доказать. Из вершины на основание опустим высоту BH. В результате получим два прямоугольных треугольника, у которых катет BH будет общим, а гипотенузы АВ и ВС равны между собой, так как являются боковыми сторонами равнобедренного треугольника.
Тогда треугольники АВН и ВСН равны по гипотенузе и катету.
В работе с прямоугольными треугольниками полезны теоремы равенства, которые значительно упрощают доказательство. Любую из них можно вывести из 3 основных теорем равенств треугольников, но это занимает лишнее время, которое можно сэкономить, просто запомнив 5 признаков равенства прямоугольных треугольников.
Раз треугольники равны, то соответствующие элементы тоже равны, то есть угол ВАН и угол ВСН равны между собой. Что и требовалось доказать.
Теорема 2
Перед формулированием теоремы, нужно сказать, что теорем всего 4, но 2, 3 и 4 похожи между собой. Поэтому докажем только 2, а остальные просто сформулируем.
В равнобедренном треугольнике высота, проведенная к основанию, является так же биссектрисой и высотой.

Проведем в треугольнике АВС высоту ВН. Она разделить треугольник на два прямоугольных, которые будут равны между собой по гипотенузе и катету, так же, как и в доказательстве первой теоремы. Если треугольники равны, значит, соответственные элементы тоже равны.
Значит отрезок AH=HC. А это значит, что BH является медианой. Так как медиана, это отрезок, соединяющий вершину треугольника и середину противоположной стороны.
Углы АВН и НВС равны, а значит, отрезком ВН угол АВС делится пополам, т.е. ВН является его биссектрисой. Биссектриса это отрезок, который делит угол пополам.
Сформулируем и запишем краткое доказательство оставшихся двух теорем.
Теорема 3
Медиана, проведенная из вершины равнобедренного треугольника, является так же высотой и биссектрисой.
В этом случае ВН будет являться медианой. Тогда сторона ВН – общая для двух треугольников, стороны АВ=ВС – по определению равнобедренного треугольника, АН=НС, так как ВН является медианой. Значит, треугольники АВН и ВСН равны по трем сторонам. Дальнейшее доказательство совпадает с теоремой 2.
Теорема 4
Биссектриса, проведенная из вершины равнобедренного треугольника, является также медианой и высотой.
Тогда, угол АВН равен углу НВС по определению биссектрисы, сторона ВН – общая, а стороны АВ=ВС – по определению. Треугольники АВН и ВСН равны по двум сторонам и углу между ними.
Как видно, теоремы говорят об одном и том же, а также имеют схожие доказательства, поэтому очень часто запоминают лишь вторую теорему, приводя ее в решении и пользуясь, при этом, всеми тремя. Подобные рассуждения ошибкой не являются.
Теорема, обратная теореме 1
Теоремы, обратные теоремам 2, 3 и 4 не имеют смысла, так как будут повторять друг друга. Но теорема, обратная теореме 1, является одним из признаков равнобедренного треугольника, поэтому может использоваться при решении.
Формулировка: Если в треугольнике два угла равны между собой, то такой треугольник является равнобедренным.
Это нужно учитывать, поскольку в задаче не всегда определяют вид треугольника, а без использования свойств в задачах на эту тему не обойтись.
Что мы узнали?
Мы разобрали 4 теоремы о свойствах равнобедренного треугольника, сформулировали обратную теорему и разобрались в доказательствах свойств. Сказали, что эти свойства характерны только для равнобедренного треугольника и использовать их для произвольной фигуры нельзя, а также разобрались в том, как просто и быстро запомнить каждое из свойств.








Комментирование закрыто