Периметр прямоугольного треугольника

Нахождение периметра прямоугольного треугольника мало чем отличается от нахождения периметра любой другой фигуры. Специализированной формулы здесь нет, разница лишь в подходах к решению задач.

Формула для нахождения периметра прямоугольного треугольника

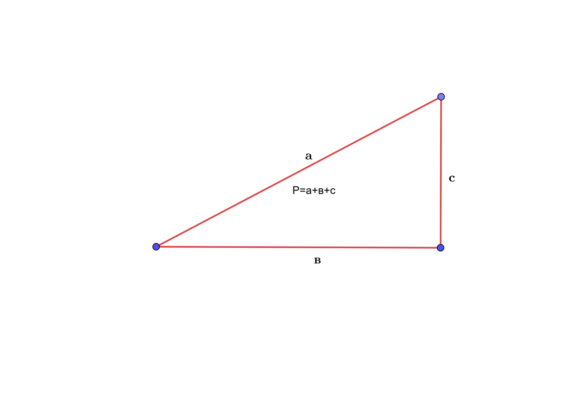
Как уже говорилось ранее, специализированных формул для периметра прямоугольного треугольника не существует. Чтобы найти периметр, нужно просто просуммировать длины всех трёх сторон.

А вот для треугольника работают тригонометрические соотношения, теорема Пифагора и ряд специальных формул площади. Эти формулы открывают целый набор подходов к решению задач, не свойственных произвольной фигуре. Рассмотрим несколько вариантов нахождения периметра прямоугольного треугольника.

Задача 1

Площадь прямоугольного треугольника можно найти как половину произведения отрезков. Значение уже есть, значит найти второй катет и гипотенузу. Пусть а=6

Тогда: $$S={1\over 2}*a*b=24$

$$S={1\более 2}*6*b=24$

$$3b=24$

б=8

Две из трех сторон известны, а гипотенузу всегда можно найти с помощью теоремы Пифагора.

$$c^2=a^2+b^2$

$$c=\sqrt{a^2+b^2}$

$$c=\sqrt{36+64}=10$

Найдем перемитер, какова длина всех стронов:

P=a+b+c=10+8+6=24

Задача 2

В этой задаче возможны два варианта. Острый угол может располагаться как на известном участке, так и напротив него. В любом случае вам придется использовать тригонометрические функции, но результаты могут отличаться. Обычно этот момент прописывается в задаче, но иногда от решателя требуется предоставить оба варианта решения. Это ясно из условия, в котором не сказано, какой из острых углов задан.

Рассмотрим вариант, в котором дан острый угол при известном угле. Затем мы используем функцию косинуса:

$$Cos(BAC)={AB\over AC}={\sqrt{3}\over2}$

$$AC={AB\over {cos(BAC)}}$

$$AC={8\over{\sqrt{3}\over 2}}={16\over\sqrt{3}}=9.24$$ – мне округлим до сотых

До н.э найдем через значение тангенса.

$$tg(BAC)={BC\над AB}={1\over\sqrt{3}}$

$$BC=AB*{1\over\sqrt{3}}={AB\over\sqrt{3}}$

$$BC={8\over\sqrt{3}}=4,62$

Расчет периметра производится по общей формуле:

Р=8+9,24+4,62=21,86

Если острый угол находится напротив известного участка, то решение будет выглядеть немного иначе.

Найдем до нашей эры через значение тангенса.

$$tg(ACB)={AB\над BC}={1\over\sqrt{3}}$

$$BC={AB\over {1\over\sqrt{3}}}=AB*\sqrt{3}=8*\sqrt{3}=13,86$

Гипотензу найдем через значение синуса.

$$sin(ACB)={AB\над AC}={1\более 2}$

$$AC={AB\over sin(ACB)}={AB\over {1\over 2}}=2*AB=2*8=16$