Окружность и круг

Круг и круг — это две разные фигуры, которые часто путают в математике в 6-м классе. Поэтому имеет смысл обсудить эту тему более подробно.

Определения

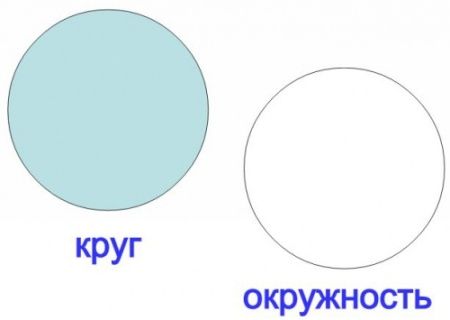
Круг – это часть пространства, ограниченная кругом. Окружность – это совокупность точек, равноудалённых от одной точки, называемой центром окружности.

Различия

Круг – это линия. Круг – плоская фигура. У круга не может быть площади, а у круга она есть.

У круга есть площадь, но в задачах мы часто ищем длину окружности. Некоторые свойства вписанной и описанной окружности треугольника связаны с длиной окружности, поэтому сложилась определенная традиция использования окружности вместо окружности. Но ни в коем случае нельзя путать эти цифры.

Сходства

Сходство заключается в характеризующих сегментах. Их несколько для круга и окружности: хорда, радиус и диаметр.

Хорда – это отрезок, соединяющий две точки окружности. Хорда может проходить через центр окружности, а может и не проходить.

Если хорда проходит через центр окружности, она называется диаметром. Диаметр – это отрезок, соединяющий две точки окружности и проходящий через центр. Диаметр используется для нахождения площади и окружности круга.

Радиус — это любой отрезок линии, соединяющий центр окружности и точку на окружности. Вместо диаметра можно использовать радиус, так как он равен его половине.

Формулы

Формула площади справедлива только для круга. Круг не может иметь площади.

$$S=\pi*r^2$

Давайте помнить это

$R={D\over{2}}$ — то есть радиус равен половине диаметра. Следовательно, это равенство можно заменить формулой площади и получить другую формулу. Или просто найдите диаметр или радиус по этой формуле и подставьте его в уже приведенную формулу.

Это формула, позволяющая найти длину окружности. Что такое окружность? Если условно выпрямить линию по кругу, то получится прямая, длину которой можно найти по формуле:

$L=\pi*d$ – диаметр, как и площадь, можно заменить диаметром.

Окружность и прямая

Расположение окружности и прямой на плоскости – отдельная тема для обсуждения. Прямая линия на плоскости может:

• Пересечь круг
• Не пересекайте круг
• Нажмите на кружок

Особый интерес представляет касательная линия, то есть линия, имеющая общую точку с окружностью. Дело в том, что эта линия обладает свойством, которое часто помогает решить проблемы.

Помните, что радиус, проведенный к точке контакта, перпендикулярен касательной.

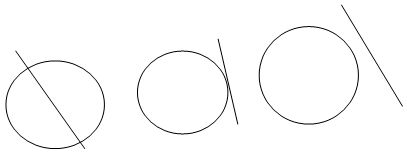
Окружность и угол

Круг и угол связаны, потому что круг является наиболее ярким примером полного угла. То есть, если нарисовать любой сегмент и повернуть его на 360 градусов вокруг начала координат, то получится круг.

Дуга измеряется углом в окружности. Дуга – это часть окружности, ограниченная двумя радиусами. Два радиуса и дуга представляют собой сектор.