
Периметр – это сумма длин всех сторон фигуры. Эта характеристика, равная площади, одинаково необходима для всех фигур. Формула периметра равнобедренного треугольника логически вытекает из его свойств, но формула не так сложна, как получение и закрепление практических навыков.
Формула вычисления периметра
Боковые стороны равнобедренного треугольника равны между собой. Это следует из определения и хорошо видно даже из названия рисунка. Именно из этого свойства вытекает формула периметра:
P=2a+b, где b — основание треугольника, а — величина боковой стороны.
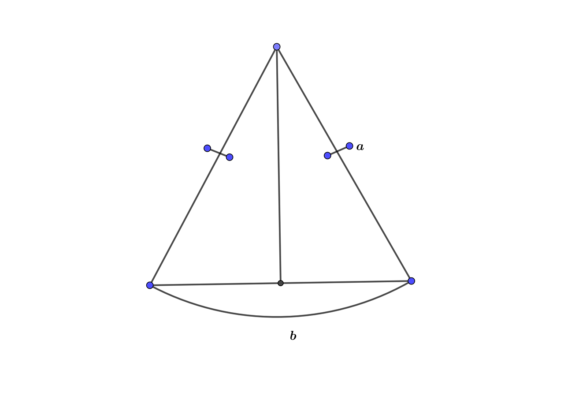
Из формулы видно, что для нахождения периметра достаточно знать размеры основания и одной из сторон. Давайте рассмотрим некоторые задачи по нахождению периметра равнобедренного треугольника. Мы будем решать задачи возрастающей сложности, это позволит вам лучше понять образ мышления, которому нужно следовать, чтобы найти периметр.
Задача 1
- В равнобедренном треугольнике основание равно 6, а приведённая к этому основанию высота равна 4. Необходимо найти периметр фигуры.
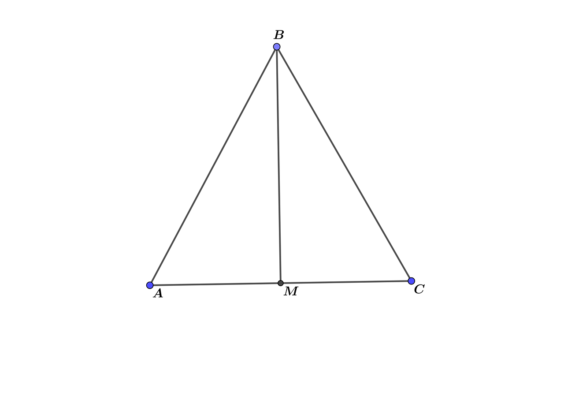
Высота равнобедренного треугольника, проведенная к основанию, является также медианой и биссектрисой. Это свойство очень часто используется при решении задач, связанных с равнобедренными треугольниками.
Треугольник АВС высоты ВМ разделен на два прямоугольных треугольника: АВМ и ВСM. В треугольнике АВМ известен катет ВМ, катет АМ равен половине основания треугольника АВС, так как ВМ – это медиана, биссектриса и высота. По теореме Пифагора находим значение гипотенузы АВ.
$$АВ^2=AM^2+BM^2$
$$AB=\sqrt{AM^2+BM^2}=\sqrt{3^2+4^2}=\sqrt{9+16}=\sqrt{25}=5$
Найдем периметр: P=AC+AB*2=6+5*2=16
Задача 2
- В равнобедренном треугольнике высота, продолженная до основания, равна 10, а острый угол при основании — 30 градусов. Вам нужно найти периметр треугольника.
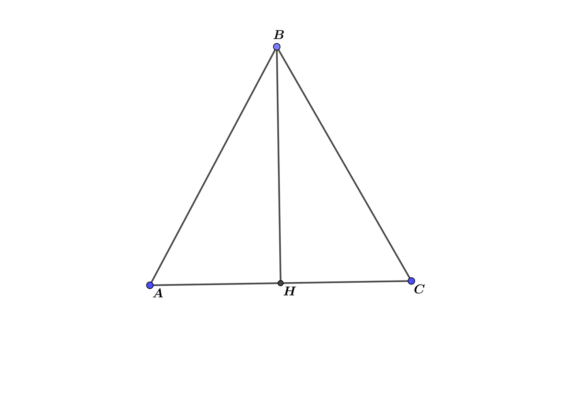
Эта задача осложняется отсутствием информации о сторонах треугольника, но, зная значение высоты и угла, можно найти сторону AH в прямоугольном треугольнике ABH, и тогда решение будет следовать формуле тот же сценарий, что и в задаче 1.
Найдем AH через значение синуса:
$$sin (ABH)={BH\over AB}={1\over2}$$ – синус 30 градусов – табличное значение.
Выражаем необходимую сторону:
$$AB={{BH\более {1\более 2}}} =BH*2=10*2=20$
Церез котангенс имеет значение АХ:
$$ctg(BAH)={AH\over BH}={1\over\sqrt{3}}$
$$AH={BH\over\sqrt{3}}=10*\sqrt{3}=17.32$$ – получившееся межной округлим до сотых.
База Найдема:
АС=АХ*2=17,32*2=34,64
Теперь, когда все необходимые значения найдены, определяем периметр:
P=AC+2*AB=34,64+2*20=74,64
Задача 3
- В равнобедренном треугольнике ABC известна площадь, равная $$16\over\sqrt{3}$$ и острый угол при основании 30 градусов. Найдите периметр треугольника.
Значения в условии часто приводятся в виде произведения корня на число. Это делается, чтобы максимально оградить последующее решение от погрешностей. Округлять результат лучше в конце вычислений
При такой постановке задачи может показаться, что решений нет, поскольку трудно выразить одну из сторон или высоту имеющихся данных. Попробуем решить по-другому.
Обратите внимание на значимую высоту и головную остановку и на латыни букрами: BH=h и AH=a
Тогда основание будет равно: AC=AH+HC=AH*2=2a
Площадь: $$S={1\более 2}*AC*BH={1\более 2}*2a*h=ah$
С другой стороны, значение h можно выразить из треугольника ABH через тангенс острого угла. Почему именно касательная? Потому что в треугольнике ABH мы уже определили два катета a и h. Необходимо выразить одно через другое. Два катета соединяют касательную и котангенс. Традиционно котангенс и косинус используются только в том случае, если тангенс или синус не подходят. Это не правило, это можно решить так, как удобно, просто, как принято.
$$tg(BAH)={h\over{a}}={1\over\sqrt{3}}$
$$h={a\over\sqrt{3}}$
Подставить полученное мжное в формулу производительности.
$$S=a*h=a*{a\over\sqrt{3}}={(a^2)\over\sqrt{3}}$
Выразим а:
$$a=\sqrt{S*\sqrt{3}}=\sqrt{16*\sqrt{3}\over\sqrt{3}}=\sqrt{16}=4$
Подставляем значение а в формулу площади и определяем значение высоты:
$$S=a*h={16\over\sqrt{3}}$
$$h={S\over{a}}={{16\over\sqrt{3}}\over{4}}={4\over\sqrt{3}}=2.31$$– полное межное округлим до сотых.
По теореме Пифагора находим боковую сторону треугольника:
$$AB^2=AH^2+BH^2$
$$AB=\sqrt{AH^2+BH^2}=\sqrt{4^2+2.31^2}=4,62$
Подставим значения в формулу периметра:
P=AB*2+AH*2=4,62*2+4*2=17,24
Что мы узнали?
Мы разобрались во всех тонкостях находнего периметра от искошестного треугольника. Они решили три задачи разного уровня сложности, показав, как решать типовые задачи по решению равнобедренного треугольника.








Комментирование закрыто