
Учащиеся часто путают трехмерные и двухмерные объекты. Это связано с тем, что на уроках математики изучаются в основном плоские фигуры, и ученик непроизвольно ищет примеры в реальной жизни, где существуют преимущественно объемные фигуры. Из-за этого часто возникает вопрос: как найти объем прямоугольника?
Формула объема прямоугольника
Вы должны запомнить раз и навсегда: формулы объема прямоугольника не существует.
Характеристики объема у прямоугольника нет, так же как нет ее и у любой двухмерной фигуры.
Аналогом объема является площадь. Но выражение «объем прямоугольника» или объем треугольника является грубой ошибкой и показывает незнание основных геометрических параметров.
Существует формула площади прямоугольника; он равен произведению длины на ширину и известен каждому чуть ли не с первого класса.
Существует также формула объема прямоугольного параллелепипеда. Это фигура, состоящая из шести граней, каждая из которых представляет собой прямоугольник. Очень часто именно эту фигуру называют прямоугольником инерции, но это ошибка, от которой необходимо избавиться.
Объем прямоугольного параллелепипеда равен произведению трех измерений: длины, ширины основания и высоты.
Объем и площадь
Объем и площадь во многом схожи понятия, но есть и разница, которую стоит понять. Район представляет собой занятую часть самолета. Если фигуру вырезать из бумаги, а затем перенести на плоскость, например на другой, более крупный лист, фигура займет определенную площадь.
Если обвести фигуру, а затем разделить полученный контур на квадраты, можно вычислить площадь фигуры.
Объем показывает пространство, которое занимает объемная фигура.
Объем прямоугольного параллелепипеда лучше всего представить так: если поместить прямоугольник в пространство, провести отрезок перпендикулярно плоскости и плавно поднять прямоугольник вверх, то результатом движения будет объем этой фигуры.

Практически любую объемную фигуру можно представить в виде результата движения плоской фигуры. Например: конус это результат движения прямоугольного треугольника вокруг одного из катетов, а цилиндр результат вращения прямоугольника вокруг своей оси. Прямоугольный параллелепипед это результат вертикального движения прямоугольника-основания вверх
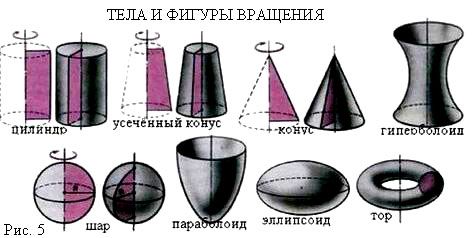
Двух и трехмерные фигуры
Как отличить двухмерную фигуру от трехмерной? Двумерная фигура существует исключительно на плоскости. Трехмерная фигура всегда содержит элементы плоских фигур: круги, линии, прямоугольники и т д.
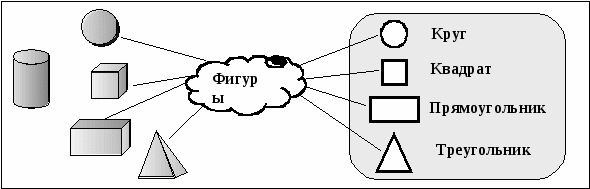
Если фигура содержит несколько плоских фигур, то фигура объемна, а если нет, то фигура состоит только из прямых, отрезков, точек и плоских углов, а саму фигуру можно изобразить на листе бумаги, как это плоская фигура.
Что мы узнали?
Мы узнали разницу между 2D и 3D формами. Мы решили, что объёма прямоугольника не существует. Это просто площадь прямоугольника или объём кубоида.








Комментирование закрыто