
В школьном курсе математики для 5 класса учащиеся знакомятся с темой о прямоугольном параллелепипеде. Это одна из первых фигур на курсе, обладающая объёмом. Именно об объеме и формуле его нахождения сегодня пойдет речь.
Определения
Прямоугольный параллелепипед – это фигура, все грани которой представляют собой прямоугольники. У фигуры шесть сторон. Грани, пересекая друг друга, образуют ребра, их 12.
Прямоугольный параллелепипед имеет четыре боковые поверхности и две поверхности основания. В жизни мы часто встречаем эту фигуру: шкаф, холодильник, ящик – все они имеют форму прямоугольного параллелепипеда.
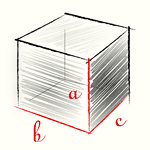
Формула объема данной фигуры
Объем куба (фигуры, все грани которого представляют собой квадраты) со стороной 1 единица называется 1 кубической единицей.

Если выложить такими кубиками низ фигуры (рис. 3), то вам понадобится 4 кубика в длину и 3 в ширину.
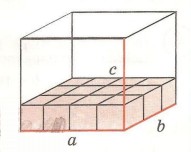
Таким образом, для заполнения базы вам понадобится:
3 х 4 = 12 – так мы посчитали площадь.
Чтобы заполнить всю фигуру и узнать объем, нужно посчитать, сколько таких слоев кубиков поместится по высоте, например, если их 2, то объем составит:
3 х 4 х 2 = 24 кубика
Итак, если учесть, что длина основания фигуры равна 4 единицам, ширина – 3, а высота – 2, то для вычитания объема прямоугольного параллелепипеда необходимо найти произведение этих величин или измерений. Фигура, имеющая три измерения, называется трехмерной или объемной.
Буква V используется для обозначения объема.
Формула объема прямоугольного параллелепипеда:
$$V = a·b·c$
При необходимости все данные в задании необходимо перевести в одни и те же единицы измерения.
Единицы измерения: $мм^3, см^3, дм^3$ и так далее. Важно правильно читать: $1 м^3$ или кубометры и так далее.
Английский иллюзионист провел 44 дня в стеклянном прямоугольном параллелепипеде, который был подвешен над рекой Темза. В его распоряжении была только вода, подушка, матрас и письменные принадлежности.
Задача: Вычислить объём фигуры, ширина которой 4 дм, длина 50 мм и высота 10 см.
Решение: Во-первых, вам необходимо преобразовать все данные в одну единицу измерения.
4 доллара дм. = 40 см$;
50 миллионов долларов. = 5 см$.
$V = а • b • h$
$V = 40 • 5 • 10 = 200 см^3$
Таким образом, объем фигуры равен $V = 200 см^3$
Для измерения объема жидкости используется специальная мерная единица – литр (1 л).
Древние измерения жидкости, например кор = 220 л, бат = 22 л.
Измерения объема:
$$1 л = 1000 см^3 = 1 дм^3$
$$1 км^3 = 1000 000 000 м^3$
$$1 м^3 = 1000 дм^3 = 1 000 000 см^3$
$$1 дм^3 = 1000 см^3$
$$1 см^3 = 1000 мм^3$
Что мы узнали?
Мы узнали, что чтобы найти объём прямоугольного параллелепипеда, надо произведение длины и ширины основания умножить на высоту фигуры. Мы также познакомились с единицами измерения объема.








Комментирование закрыто