
Основание треугольника — та же сторона, что и две другие. Фундамент редко имеет особое значение, но из-за его визуальной изоляции от других сторон студенты часто путаются и допускают ошибки. Разберем подробнее, как сторону треугольника можно считать основанием, и в каких случаях это действительно имеет значение
Стороны треугольника
У треугольника всегда три стороны. Одно из них считается основой. Как регило, просмотр отдыха происходит только постранением, т.е нижнюю сторону треугольника, и она принимается за основание.
Иногда в решении указывают углы при основании произвольного треугольника. Это не совсем верно, поскольку в произвольном треугольнике все углы равнозначны, а значит не имеет смысла выделять углы при основании. Выделяются только углы при основании равнобедренного треугольника.
Необходимо учитывать, что любой произвольный треугольник можно условно перевернуть, т.е перечить фигуру таким образом, чтобы вторая сторона стала основой. Поэтому разделять понятия боковых сторон и основания произвольного треугольника нет смысла – это только внесет путаницу в решение задачи.
Уравнение основания треугольника, так же, как и уравнение любой из сторон треугольника, является уравнением прямой линии.
Равнобедренный треугольник
Равнобедренный треугольник — единственный тип треугольника, имеющий реальное практическое значение. Равнобедренным треугольником называется треугольник, две стороны которого равны друг другу. Прямые стороны называются сторонами, а третья сторона считается основанием.
На основе равнобедренного треугольника существуют две теоремы. Этот:
- Теорема о равенстве углов: в равнобедренном треугольнике углы при основании равны.
- Теорема о равенстве медиан, биссектрис и высот, отнесенных к основанию. В теореме особо подчеркивается, что из трех возможных медиан, высот и биссектрис только те, которые проведены к основанию, окажутся равными между собой.
В равнобедренном треугольнике основание определяется значением сторон: равные строны – боковые, неравная – основание.
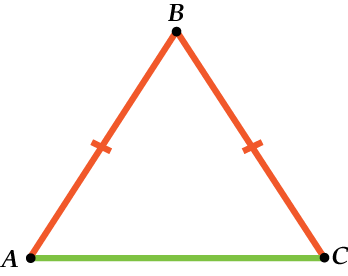
По ходу решения задачи может получится так, что основание окажется сбоку, не нужно этого пугаться. Стоит или привыкнуть к такому построению равнобедренного треугольника или каждый раз перечерчивать чертеж, разворачивая треугольник в нужную сторону.
Равносторонний треугольник
Равносторонний треугольник является частным случаем равнобедренного треугольника. В равнобедренном треугольнике две стороны равны, а в равностороннем треугольнике равны все три. Но именно из-за этого свойства теряется значение основания равнобедренного треугольника.
В равностороннем треугольнике не выбирайте ни одну сторону: две другие всегда будут равны между собой, а потому основанием можно считать любую сторону.
Существует формула, где часто упоминается слово основание. Это формула площади, которая равна половине произведения основания треугольника на высоту, проведенную к этому основанию. Но в качестве основания может быть принята любая сторона, главное, чтобы именно на нее падала высота. Поэтому и в этом случае выбор стороны треугольника, которую можно считать основанием, некритичен.
Что мы узнали?
Мы узнали, что такое основание треугольника. Говорили о ситуациях, когда необходимо выделить основание других сторон треугольника, и когда это оказывается пустой тратой времени. Обсудили программы «Остановка онлайн треугольника.








Комментирование закрыто