
В 5-м классе по математике довольно много многоугольников. Только самые популярные из них имеют имена. Давайте рассмотрим наиболее распространенные виды многоугольников.
Что такое многоугольник?
Фактически любую фигуру можно считать многоугольником. И плоские, и объемные. Ведь в любой фигуре количество углов больше или равно 3. Многоугольники делятся на выпуклые и невыпуклые. Этот параметр определяется следующим образом: через каждую сторону проводится прямая линия. Если фигура каждой прямой лежит по одну сторону от прямой, то многоугольник называется выпуклым.
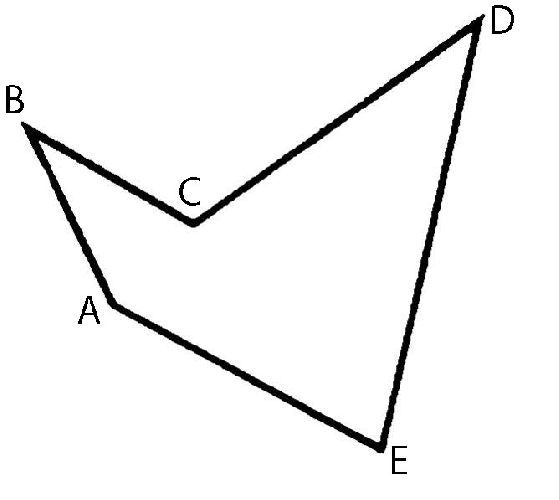
В школьном курсе нет ни одной теоремы для невыпуклых многоугольников. Далеко не каждый профессор математики может вспомнить хотя бы одну такую теорему. Дело в том, что в жизни невыпуклые треугольники не встречаются и решать задачи на них просто не имеет смысла. Но знать о разделении многоугольников по такому признаку – обязательно.
Виды многоугольников
Простейшие многоугольники делятся по количеству углов:
- Треугольник.
- Квадрат.
- Пентагон.
На самом деле названия можно продолжать до бесконечности, но даже пятиугольник при решении задач встречается редко, при его решении часто приходится пользоваться уравнениями.
Пятиугольник редко встречается и в строительстве, физике и прочих науках. В любом случае, если ученику требуется решить пятиугольник, его нужно разбить на треугольники и работать с привычными фигурами. А на треугольники можно разбить вообще любую плоскую фигуру.
Треугольник
Треугольник – это не только самый простой многоугольник, но и основа самой известной геометрии. При решении все неизвестные фигуры плана разбиваются на треугольники. Для этой фигуры обнаружено большинство теорем, характеризующих точки, отрезки и пропорции. В Америке существует целая энциклопедия треугольников.
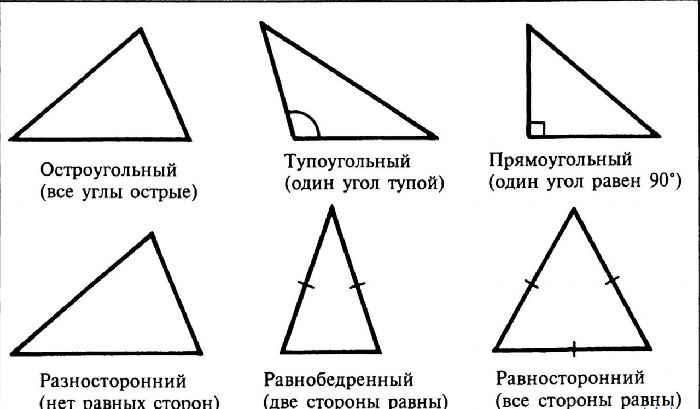
В зависимости от углов, входящих в треугольник, фигуры делятся на:
- Остро угловатый.
- Прямоугольный.
- Тупой.
В зависимости от сторон треугольники делятся на:
- Произвольный.
- Прямая нога.
- Равносторонние или обычные.
Особое внимание следует уделить правильному определению типов треугольников. Многие теоремы предназначены для определенного типа треугольников и не работают с другими.
Четырехугольник
Квадрат имеет не меньше вариаций, чем треугольник. Но основных всего два: параллелограмм и трапеция.
Параллелограмм – это выпуклый четырехугольник, стороны которого попарно равны и параллельны. Обратите внимание, что в определении треугольника никогда не используется параметр «выпуклость», о котором мы говорили вначале. Дело в том, что треугольники всегда выпуклые, но квадраты могут быть и невыпуклыми.
Параллелограмм в зависимости от подобия элементов: углов и сторон делится на следующие фигуры:
- Квадрат.
- Прямоугольник.
- Ромб.
- Произвольный параллелограмм.
Все эти знакомые фигуры являются вариациями параллелограммов.

Трапеция – это квадрат, у которого две стороны параллельны, а две – нет. Также есть множество квадратов, не входящих ни в одну из групп. Такие фигуры называются произвольными квадратами.
Необычные многогранники
Помимо упомянутых выше цифр, есть и множество других. Число углов в многоугольнике может быть бесконечно большим, но найти такие фигуры можно только при использовании правила многоугольника. Это правило используется при добавлении вектора.
Существует отдельное понятие правильных многоугольников, т.е фигур, у которых все стороны и углы равны. Плоские фигуры на гранях объемных предметов образуют многогранники с замысловатыми названиями:
- Тетраэдр.
- Октаэдры.
- Додекаэдр.
Что мы узнали?
Мы говорили о полигонах. Мы выделили основные типы полигонов и немного рассказали о каждом типе. Объяснили, почему нужно точно знать, какой тип многоугольника указан в задаче.








Комментирование закрыто