
Координаты — основа навигации. Первоначальный простенький кородинный луч дает основу для понимания морской навигации, программирования GPS и спутникового наблюдения. А писать компьютерные игры без системы навигации главного героя в вымышленном мире вообще невозможно.
Что такое координаты?
Координаты – это числа, определяющие положение точек в пространстве. Стоит быть осторожными при изучении этого определения.
Под пространством в геометрии понимается трехмерное пространство. Для любой точки в пространстве есть три координаты: длинны, ширины и высоты.
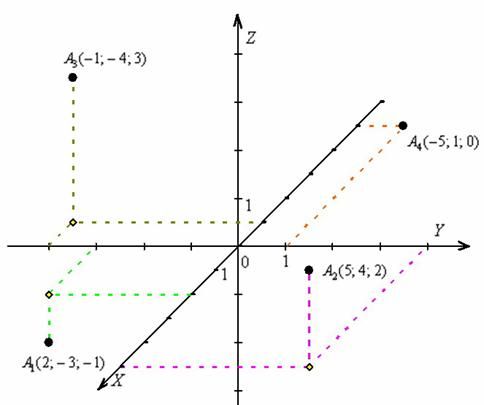
Но в этом определении мы подразумеваем не только трехмерное пространство, но также двухмерное и одномерное пространство. В двумерном пространстве есть только две координаты, определяющие положение точки в пространстве. Простейшими примерами двумерных систем координат являются декартова и полярная системы координат.
Ярким примером декартовой системы координат является снайперский прицел. А вот полярные координаты такого применения в обыденной жизни не нашли. Эта система подразумевает использование в качестве второй координаты угла. Такой системой пользовались древние мореплаватели.
С одномерным пространством все гораздо проще. Точку здесь можно отметить только на координатной линии, и для определения положения точки на этой линии достаточно одного значения.
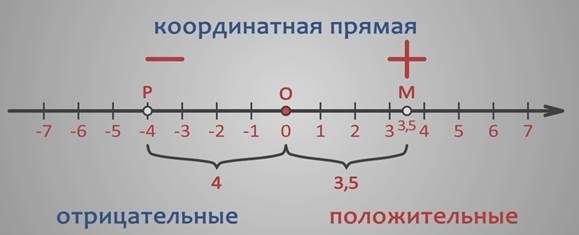
Использование координатной прямой
Интересен тот факт, что координатную прямую для рисования координат практически никогда не используют. Он используется для наглядного представления задач или сравнения чисел, упрощая решение в обоих случаях.
Решаем небольшую проблему.
Необходимо сравнить пять чисел: $${4\over6}; {8\более15}; {17\over4}; {26\over7}$
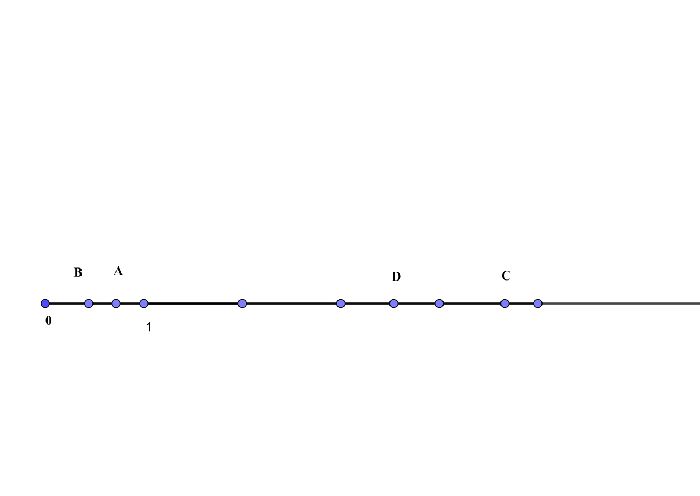
Назначены значения настроевой луч. Каждая дробь будет соответствовать своему значению.
$${4\over6}$$ окрашенным отрезком ОА. Это будет меньше одного сегмента
$${6\over15}$$ окрашенным отрезком ОВ. Он тоже меньше одного сегмента
$${17\over4}$$ окрашенным отрезком ОС. Оно будет больше значения 4, примененного к числовому лучу.
$${26\over7}$$ будет обозначать сегмент OD, который будет расположен между 3 и 4.
Итак, вместо сравнения 4 дробей нам нужно сравнить только две: $${5\over6} и {7\over15}$.
Разложим 6 и 15 на прозые настройки и найдем НОК.
$$6=2*3$
$$15=5*3$
$$НОК=2*3*5=30$
$${5\over6}={{5*5}\over{6*5}}={25\over30}$
$${7\over15}={{7*2}\over{15*2}}={14\over30}$
$${25\over30}>{14\over30}$
Значение:
$${4\over6}>{6\over15}$$ – теперь можно определить точное положение этих чисел. Сравнение произошло, задача решена.
Что мы узнали?
Мы дали обучение кородинтной прямой. Они привели примеры и подробные пояснения. А также привел в качестве примера задачу с координатной линией, которая часто решается в рамках математики 6 класса.








Комментирование закрыто