
С самой распространенной фигурой по математике школьники сталкиваются в начальной школе. Но со временем знакомишься и с более серьезным вариантом расчета элементов треугольника.
Определение
Треугольник – это многоугольник с тремя сторонами и тремя углами. Основными элементами этой геометрической фигуры являются отрезки, вершины и углы. Для решения некоторых задач могут потребоваться дополнительные конструкции.
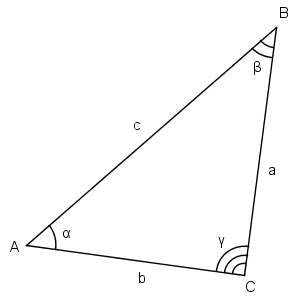
Рассматриваемое понятие часто обобщается в зависимости от поставленных целей. Например, треугольник можно представить тремя точками, соединенными отрезками и не лежащими на одной прямой.
Используя сходство между элементами треугольника, эту геометрическую фигуру можно отнести к определенному типу. Например, если все стороны треугольника равны, такой треугольник называется равносторонним. С другой стороны, сходство элементов двух треугольников тоже может помочь. Это доказывает сходство и подобие фигур.
Общая теория геометрии различных треугольников возникла еще во времена Древней Греции.
Характеристики понятия
Обозначение стороны треугольника традиционно производится от названий вершин, которые содержит та или иная сторона. Углы треугольника также обозначаются вершинами.
Значение
Вообще для определения соответствия заданных геометрических фигур используются такие элементы, как:
- две стороны и угол между ними;
- три стороны;
- одна сторона и прилегающие углы.
В случае прямоугольных треугольников их подобие доказывается с помощью следующих параметров:
- по тем же значениям две ноги;
- с помощью сравнения длины катета и гипотенузы;
- сравнить один из острых углов и гипотенузу;
- с помощью сравнения длин гипотенузы и катета.
Основные свойства основных элементов треугольника касаются сторон и углов. Более того, часто возникает необходимость построения дополнительного внешнего угла для упрощения расчетов других параметров.
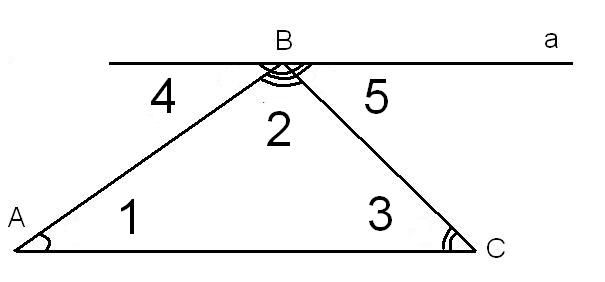
Треугольники часто рассматривают вместе с их внутренним пространством, что требуется при определении площади геометрической фигуры.
Взаимосвязь основных элементов треугольника
Числовую геометрическую характеристику данной фигуры на плоскости можно определить, используя определенные данные о ее параметрах.
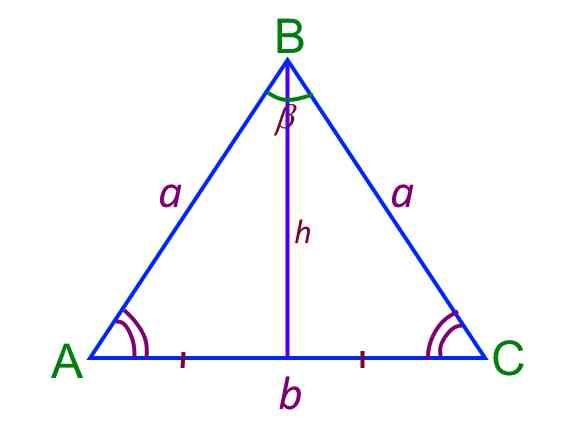
$$S=bra_b$
$$S=a_2sinβ$
Что мы узнали?
Треугольник состоит из элементов, используемых в сложных вычислениях. С их помощью можно найти площадь рассматриваемой фигуры, а также доказать ряд теорем.








Комментирование закрыто