
В этой статье мы поговорим о длине прямоугольника. Как определить, какая сторона является длиной и зачем их разделять. Давайте рассмотрим три способа найти длину прямоугольника и решим небольшую задачку.
Что такое длина прямоугольника
Довольно часто люди путают длину и ширину прямоугольника; как правило, это не критично, но в результате существенно снижается наглядность, и как следствие страдает качество решения.
Прямоугольник — частный случай параллелограмма. Параллелограмм, каждый угол которого равен 90 градусам, называется прямоугольником. Для визуального представления было бы лучше, если бы длина выступала в качестве нижней опоры прямоугольника. Бывает так, что такой рисунок больше всего напоминает рисунки в учебнике, и поэтому ученику будет легче понять тему.
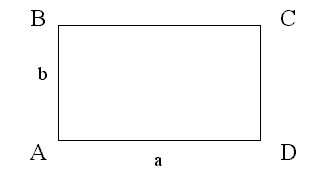
Три способа найти длину прямоугольника
Если разделить фигуру на две части диагональю, то вы заметите, что прямоугольник разделен на два прямоугольных треугольника. Из этого деления следуют все формулы длины прямоугольника.
-
Через теорему Пифагора
Если известны длина диагонали (обозначим ее буквой d) и длина прямоугольника (примем за значение букву а). Тогда квадратный корень из разности квадратов диагонали и длины будет равен ширине прямоугольника.
Чтобы было понятнее, запишем решение в виде нескольких формул.
По теореме Пифагора квадрат гипотенузы равен сумме квадратов катетов. Гипотенуза – это сторона, противолежащая прямому углу, две другие стороны называются катетами. В нашем случае гипотенузой является диагональ.
Это означает: d2=a2+b2. Из этого выражения выражаем квадрат ширины (значение «b»): b2=d2-a2
Чтобы определить значение b, извлеките квадратный корень из обеих частей полученного выражения: b=(d2-a2)(-1)
В случае необходимости, можно поменять местами а и b, тогда получится формула длины.
-
Через площадь
Рассмотрим еще один способ нахождения длины прямоугольника – через площадь. Площадь прямоугольника равна произведению его длины и ширины. То есть использовать уже известное обозначение S=a*b. Выразим значение ширины по этой формуле: b=S/b.
Как и в первом методе, вы можете поменять местами a и b, чтобы получить формулу длины: a=S/b.
-
Тригонометрическая функция
Один из самых быстрых, но немного более сложных способов найти длину — использовать тригонометрическую функцию.
Если это прямоугольный треугольник, соответствующее соотношение называется синусом и косинусом.
Давайте выберем угол между длиной и диагональю. Обозначим его α. Тогда sin α равен отношению катета, лежащего против угла α, к гипотенузе: Sin α = a/c
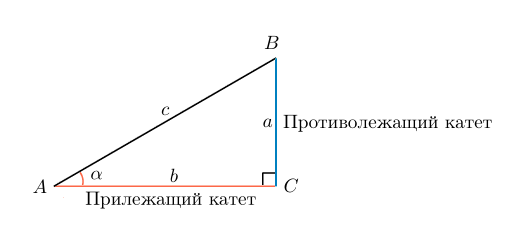
Значение синуса любого угла можно найти в таблицах Брадиса или с помощью калькулятора. Для удобства можно воспользоваться онлайн-версией, которая найдет значение отношения автоматически.
Но в формуле нет значения b, соответствующего длине, поэтому мы воспользуемся основным тригонометрическим тождеством. Косинус — это отношение стороны, лежащей рядом с углом, к гипотенузе: cos a=b/c
Это значит, что длину можно найти, умножив косинус на гипотенузу: b=cos α*c
Задача
- Найдите длину прямоугольника, если известно, что его ширина равна 3, а диагональ равна 5.
Воспользуемся теоремой Пифагора и найдем b. Длина равна квадратному корню из разности квадрата диагонали и квадрата ширины.
5^2=25
3^2=9
25-9=16
Квадратный корень из 16 равен 4.
Значение б=4
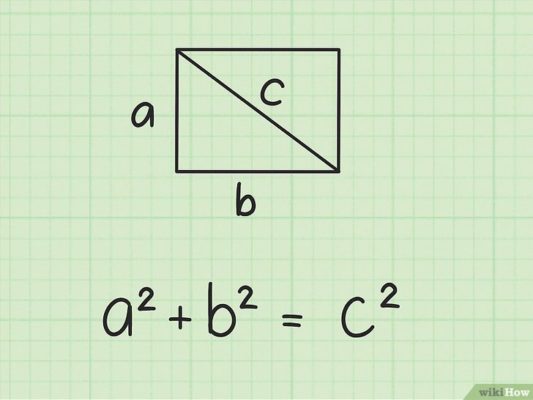
Что мы узнали?
Мы рассмотрели, как правильно нарисовать прямоугольник для большей наглядности, рассмотрели, как найти длину или ширину при разных условиях задачи, и решили задачу средней сложности на нахождение длины прямоугольника с помощью теоремы Пифагора.








Комментирование закрыто