Диагональ треугольника

Очень часто в начале изучения фигуры учащиеся путают значение диагонали прямоугольника и треугольника. Поэтому, чтобы не запутаться в обозначениях, лучше раз и навсегда разобраться в предмете.

Треугольник

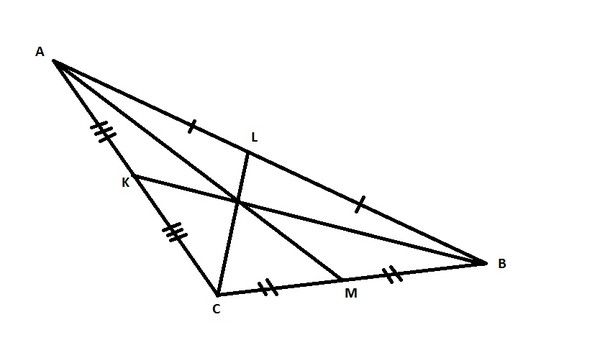
Треугольник – это фигура, состоящая из трёх сторон и трёх углов. Треугольник имеет три характерных сегмента:

• Высота;
• Медиана;
• Биссектриса.

В принципе, в треугольнике не может быть диагонали. Дело в том, что диагонали можно рисовать только в многоугольниках, у которых больше 3 сторон.

Почему? Потому что диагональ – это отрезок, соединяющий противоположные углы. В треугольнике нет и не может быть противоположных вершин. Противоположная вершине сторона есть, но сами вершины всегда смежны, т.е соединены с одной стороны. Это означает, что в треугольнике нет диагонали

Прямоугольник

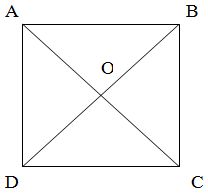
Прямоугольник — первая фигура в школьном курсе математики, имеющая диагональ. Точно так же, как у квадрата есть диагональ.

Диагональ прямоугольника или квадрата всегда равна:

• Делит фигуру на два равных прямоугольных треугольника.
• В получившихся треугольниках диагональ будет гипотенузой
• Диагональ будет равна квадратному корню из суммы квадратов катетов по теореме Пифагора

Однако это правило не распространяется на другие квадраты. Например, диагонали параллелограмма всегда не равны друг другу. Помните, если перед вами произвольный квадрат, вы не можете без доказательства использовать утверждение о равенстве диагоналей. Каждое утверждение в геометрии, кроме аксиом, должно быть доказано.

Кроме прямоугольника и квадрата, у ромба равные диагонали. В этом случае диагонали ромба перпендикулярны друг другу и, как и диагонали квадрата и прямоугольника, делятся пополам точкой пересечения.

Многоугольник

Фактически любую фигуру, имеющую более двух углов, можно назвать многоугольником. На самом деле многоугольником можно назвать любую фигуру, поскольку замкнутая фигура не может иметь 2 угла.

Рассмотрим многоугольники, имеющие более 4 углов, поскольку мы уже рассматривали квадраты.

В многоугольнике, если он неправильный, без дополнительных построений не удастся решить задачу нахождения диагонали. В правильном многоугольнике все диагонали равны между собой, а точка пересечения делится пополам.

Количество диагоналей можно рассчитать, оценив количество смежных и несмежных вершин. Вершины, соединенные одним отрезком, называются смежными.

Например, в четырехугольнике любая вершина имеет две соседние вершины. Это означает, что для каждой вершины существует только одна диагональ. Диагональ соединяет два противоположных угла, всего углов 4, значит 4:2=2 – в любом квадрате 2 диагонали.

Но этот метод не сработает, если задача требует подсчета количества диагоналей многоугольника с 5989 сторонами. Такая цифра вполне возможна в теории. На практике рисовать его очень утомительно, как и рассчитывать диагонали рисунка. Таким образом, была выведена формула числа диагоналей многоугольника:

$P={n(n-3)\over{2}}$ – где n — количество сторон многоугольника.

Ищем квадрат:

$P={4(4-3)\over{2}}={4\over2}=2$ — всё правильно.