
Отрезок – это часть прямой. В математике тема отрезков имеет большое значение: с их помощью строят фигуры, с помощью отрезков рисуют картинки к задачам и сравнивают числа. Давайте поговорим об отрезках и о том, как их использовать в математике в 5-м классе.
Определение
Отрезок – это часть прямой, ограниченная двумя точками. Это означает, что в отличие от прямой или луча отрезок конечен и не имеет направления. Числовая черта на числовой прямой или числовой прямой означает определенное число. Для сравнения чисел можно использовать числовые линии.
Числовой луч обычно принимается для сравнения положительных чисел. Если среди ряда чисел, которые необходимо сравнить, есть отрицательные значения – правильнее будет воспользоваться числовой прямой.
Сегмент всегда имеет определенное значение. Прямую линию или луч невозможно определить конечным числом в метрах или сантиметрах, поэтому во всех современных расчетах, как теоретических, так и практических, используются отрезки.
Задача на построение
Построим треугольник со сторонами 3, 5 и 4. Каждая сторона представляет собой отрезок заданного размера. Это еще одно свойство сегментов. Используя три отрезка заданного размера, всегда можно построить треугольник.
Сначала нарисуем отрезок AB=3. Вы можете выбрать любое другое значение из предложенных.
Конкретно в этой задаче такой подбор чисел выполнен для возможности дальнейшей проверки.
Возьмем точку А за центр круга радиуса 4 и нарисуем ее. Тогда точку В возьмем за центр окружности радиусом 5. На пересечении двух окружностей получим точку С – третью точку треугольника.
Треугольник со сторонами 3, 4 и 5 – это классический прямоугольный треугольник. Соответственно с катетами 3, 4 и гипотенузой 5. Эти пропорции были выведены еще в Древней Греции и сегодня очень часто применяются в простых задачах на решение прямоугольных треугольников.
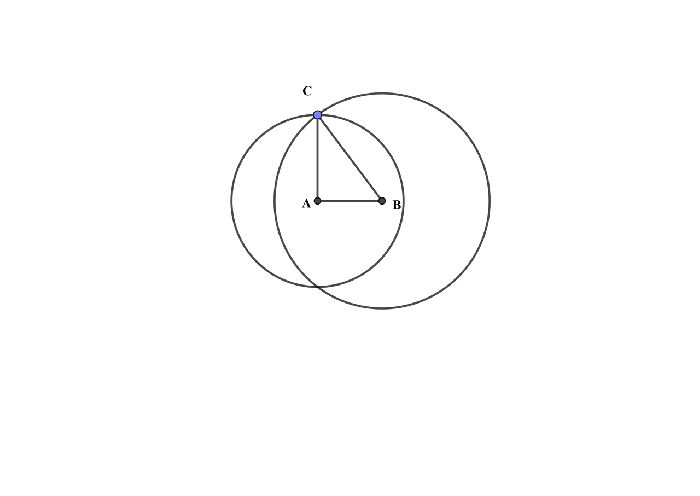
В частности, в нашем случае это означает, что полученный треугольник должен быть прямоугольным согласно обратной теореме Пифагора.
Давай проверим:
$$5^2=3^2+4^2$
$$25=9+16$
25=25 – все верно, условие выполнено. А на рисунке визуально видно, что треугольник построен правильно. Строя произвольный треугольник с тремя заданными отрезками, заранее убедитесь, что в треугольнике выполняются условия неравенства: одна сторона всегда меньше суммы двух других сторон.
Задача с числовым лучом
Для сравнения необходимо пять чисел: ${5\over6}; {7\более15}; {18\овер4}; {25\более7}$
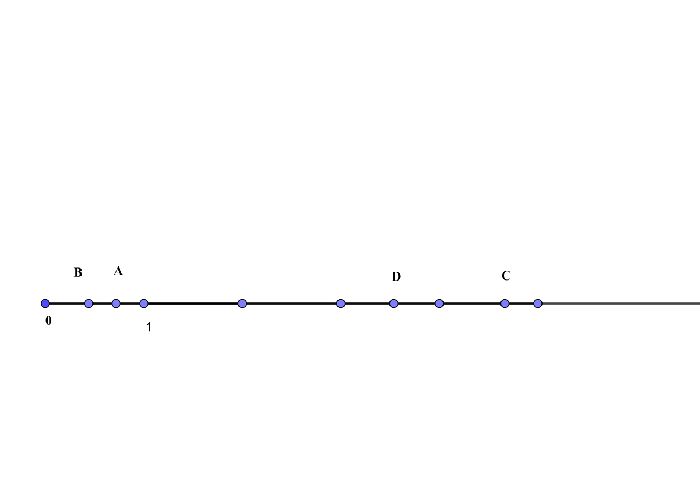
Построим значения на числовой прямой. Каждая дробь будет иметь свое значение.
Обозначим $${5\over6}$$ отрезком OA. Это будет меньше единичного сегмента
Обозначим $${7\over15}$$ отрезком OB. Он также меньше единичного сегмента
Обозначим $${18\over4}$$ отрезком OS. Оно будет больше значения 4, напечатанного на числовой строке.
$${25\over7}$$ будет отмечен сегментом OD, который будет расположен между 3 и 4.
Это означает, что вместо сравнения 4 дробей нам нужно сравнить только две: ${5\over6}$ и ${7\over15}$.
Давайте разложим 6 и 15 на простые числа и найдем НОК.
$$6=2*3$
$$15=5*3$
$$NOK=2*3*5=30$
$${5\over6}={{5*5}\over{6*5}}={25\over30}$
$${7\over15}={{7*2}\over{15*2}}={14\over30}$
$${25\over30}>{14\over30}$
Средства:
${5\over6}>{7\over15}$ — теперь вы можете указать точное положение этих цифр. Сравнение завершено, проблема решена.
Что мы узнали?
Мы выяснили, что такое отрезок в математике, выделили отличие от луча и прямой. Мы определили возможность использования его в геометрии для построения треугольников по значениям сторон и в математике для сравнения рядов дробей.








Комментирование закрыто