
Симметрия сопровождает человека на протяжении всей жизни все время: в архитектуре, технике, искусстве и медицине. Понятие симметрии понятно каждому на интуитивном уровне, но сегодня мы разберем понятие симметрии в пространстве с точки зрения геометрии.
Что такое симметрия?
Симметрия – это свойство геометрических фигур, расположенных на одинаковом расстоянии по отношению к определенной точке (центру симметрии) или прямой линии (оси симметрии). Выделяют три основных типа симметрии:
- Симметрия относительно точки или центральная симметрия.
- Симметрия – это относительно прямая или осевая симметрия.
- Симметрия относительно плоскости, также называемая плоской или зеркальной симметрией.
В архитектуре существует множество расширенных определений из геометрии. Это позволяет архитекторам проектировать красивые и функциональные здания. Так, в архитектуре выделяют понятия симметрии движения, разделяя ее на переносную и поворотную симметрии.
Центральная симметрия
Чтобы проверить, симметрична ли одна фигура другой относительно точки, следует провести линию из каждой точки объекта через центр симметрии другой фигуры.
Если обозначить такой отрезок АВ, а центр симметрии точкой О, то объекты можно назвать симметричными, если АО = ОВ, то есть если точка О находится в середине такого отрезка. При этом проверяется каждый сегмент между каждой точкой объектов симметрии. Если условия для каждого объекта совпадают, объекты считаются симметричными.
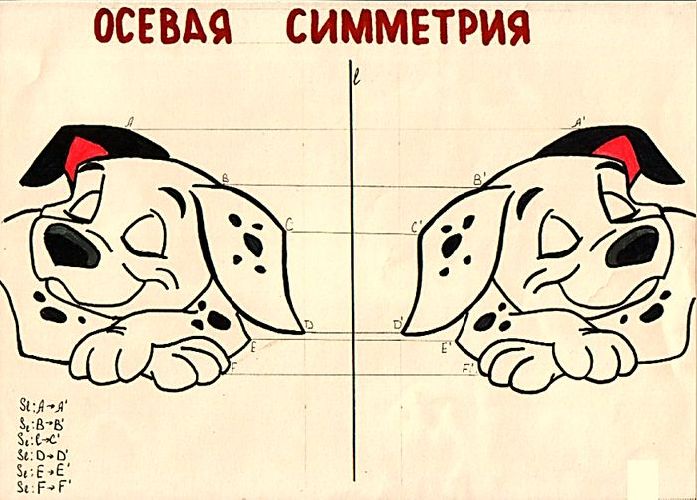
Осевая симметрия
Чтобы проверить, симметрична ли одна фигура другой относительно оси, следует провести отрезок от каждой точки одного объекта до соответствующей точки другого.
Этот отрезок должен быть перпендикулярен оси симметрии, а также разделять ось симметрии пополам. Если для каждого из сегментов выполняются оба условия: объекты считаются симметричными относительно оси.
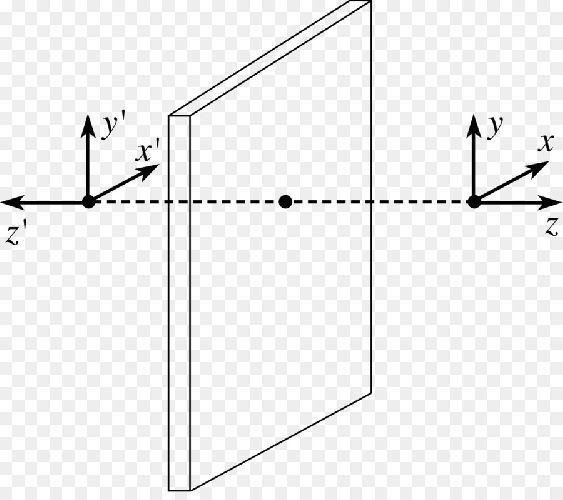
Симметрия в пространстве
Плоская симметрия — более интересная тема, чем плоская симметрия, но основы остаются теми же.
Плоскость в пространстве является аналогом прямой в плоскости, поэтому многие принципы работы с прямыми в плоскости переносятся на пространство.
Чтобы определить, симметричен ли объект в пространстве другому относительно плоскости, следует провести прямую линию от каждой точки объекта к каждой соответствующей точке другого объекта. Эта линия должна пересекать плоскость и быть перпендикулярной ей. Тогда, если плоскость делит прямую на два равных отрезка, объекты считаются симметричными относительно плоскости.
В этом случае плоскость становится условным зеркалом, отражающим один предмет по отношению к другому, поэтому симметрию называют зеркальной симметрией. Именно поэтому самым ярким примером зеркальной симметрии считается отражение в зеркале.
Что мы узнали?
Мы вспомнили все виды симметрии, обсудили различия между видами симметрии на плоскости и в пространстве. Мне рассказали, как определить симметричность двух объектов относительно точки, линии и плоскости. Отдельно мы говорили о зеркальной симметрии относительно плоскости.








Комментирование закрыто